
����Ŀ��Ϊ��ǿ��ѧ���Ļ�����ʶ��ijУ��ί��ȫУ�ٰ��ˡ�������������������֪ʶ��������������и��ݳ����ɼ�����ѡ��5��ѡ����ɳ��д����Ӻ��д����ӽ��и�����������ѧ���ĸ����ɼ�������10�֣���ͼ��ʾ��
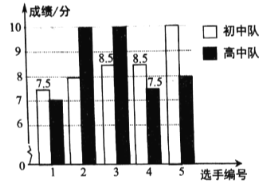
��1������ͼʾ��д�±���
ƽ���� | ��λ�� | ���� | ���� | |
���ж� | 8.5 | 0.7 | ||
���ж� | 8.5 | 10 |
��2��С��ͬѧ˵������θ����ҵ���8�֣������Ƕ�������������ƫ�£���С���dz��жӻ��Ǹ��жӵ�ѧ����Ϊʲô��
��3��������ӳɼ���ƽ���֡���λ���ͷ�������ĸ��Եĸ����ɼ��Ϻã�
���𰸡���1��8.5��8.5��8��1.6����2��С���ڳ��жӣ����ɼ���������3�����жӵijɼ���Щ�����ɼ�����
��������
��1��������ͼ�ó����жӺ��жӳɼ����ٸ���ƽ��������λ��������������ĸ������ɵã�
��2��������λ�����������ɵã�
��3����ƽ��������λ����������������ɵã�
��1������1��������ͳ��ͼ֪�����жӳɼ����£�7.5��8��8.5��8.5��10�����жӵijɼ�Ϊ��7��7.5��8��10��10��
���Գ��жӵ�ƽ����Ϊ![]() ������Ϊ8.5��
������Ϊ8.5��
���жӵ���λ��Ϊ8������Ϊ![]() ��[��7-8.5��2+��7.5-8.5��2+��8-8.5��2+2����10-8.5��2]=1.6��
��[��7-8.5��2+��7.5-8.5��2+��8-8.5��2+2����10-8.5��2]=1.6��
��ȫ�������£�
ƽ���� | ��λ�� | ���� | ���� | |
���ж� | 8.5 | 8.5 | 8.5 | 0.7 |
���ж� | 8.5 | 8 | 10 | 1.6 |
��2��С���ڳ��жӣ�
���ɣ����ݣ�1����֪�����С����жӵ���λ���ֱ�Ϊ8.5�ֺ�8�֣�
��8��8.5��
��С���ڳ��жӣ�
��3�����жӵijɼ���Щ����Ϊ�����ӵ�ƽ������ͬ�����жӵ���λ���ߣ����ҳ��жӵķ���С�ڸ��жӵķ��������ƽ������ͬ���������λ���ߡ�����С�ij��жӳɼ��Ϻã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1�����ⷢ��
��ͼ1������OAB����OCD�У�OA=OB��OC=OD����AOB=��COD=40��������AC��BD���ڵ�M����գ�
��![]() ��ֵΪ�� ����
��ֵΪ�� ����
�ڡ�AMB�Ķ���Ϊ�� ����
��2�����̽��
��ͼ2������OAB����OCD�У���AOB=��COD=90�㣬��OAB=��OCD=30��������AC��BD���ӳ����ڵ�M�����ж�![]() ��ֵ����AMB�Ķ�������˵�����ɣ�
��ֵ����AMB�Ķ�������˵�����ɣ�
��3����չ����
�ڣ�2���������£�����OCD�Ƶ�O��ƽ������ת��AC��BD����ֱ�߽��ڵ�M����OD=1��OB=![]() ����ֱ��д������C���M�غ�ʱAC�ij���
����ֱ��д������C���M�غ�ʱAC�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
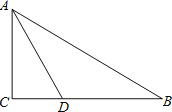
����Ŀ����֪����ͼ����![]() �У�
�У�![]() �Ľ�ƽ����
�Ľ�ƽ����![]() ��
��![]() ����
����![]() ��
��
��1����![]() ����һ��
����һ��![]() ΪԲ�ģ���
ΪԲ�ģ���![]() ������
������![]() ����д������������ͼ�ۼ��������ж�ֱ��
����д������������ͼ�ۼ��������ж�ֱ��![]() ��
��![]() ��λ�ù�ϵ����˵�����ɣ�
��λ�ù�ϵ����˵�����ɣ�
��2������1���е�![]() ��
��![]() �ߵ���һ������Ϊ
�ߵ���һ������Ϊ![]() ��
��![]() �����߶�
�����߶�![]() ���ӻ�
���ӻ�![]() ��Χ�ɵ�ͼ�������������������ź�
��Χ�ɵ�ͼ�������������������ź�![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�OΪ��ABCD�ĶԳ����ģ���A������Ϊ(��2����2)��AB=5��AB//x�ᣬ����������y=![]() ��ͼ����D������ABCD��y������ƽ�ƣ�ʹ��C�Ķ�Ӧ��C�����ڷ�����������ͼ���ϣ���ƽ�ƹ������߶�ACɨ�������Ϊ(����)
��ͼ����D������ABCD��y������ƽ�ƣ�ʹ��C�Ķ�Ӧ��C�����ڷ�����������ͼ���ϣ���ƽ�ƹ������߶�ACɨ�������Ϊ(����)
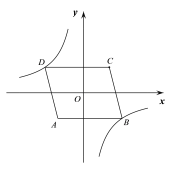
A.10B.18C.20D.24
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
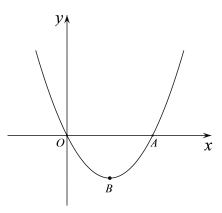
����Ŀ����ͼ��������y=x2+mx��m<0����x����O��A���㣬����Ϊ��B��
��1�����AOB��������ú�m�Ĵ���ʽ��ʾ����
��2��ֱ��y=kx+b��k��0������B�����������߽�����һ��D����D���A���غϣ�����y���ڵ�C������C��CE��AB��x���ڵ�E��
������ ����OBA=90����2<![]() <3����k��ȡֵ��Χ��
<3����k��ȡֵ��Χ��
������ ��֤��DE��y�ᣮ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У����κ���y��ax2+bx+c��a��0����ͼ����ͼ��ʾ���ָ����½��ۣ���abc��0����c+2a��0����9a��3b+c��0����a��b��m��am+b����mΪʵ��������4ac��b2��0�����д�����۵ĸ����У�������
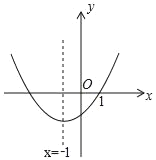
A.1��B.2��C.3��D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������![]() ����A��-1,0��B��4��0����C��0��4�����㣮
����A��-1,0��B��4��0����C��0��4�����㣮
��1���������ߵĽ���ʽ������D�����ꣻ
��2������1���е�����������ƽ��![]() �����ȵ�λ��������ƽ��h(h��0)�����ȵ�λ���õ��������ߣ����������ߵĶ���
�����ȵ�λ��������ƽ��h(h��0)�����ȵ�λ���õ��������ߣ����������ߵĶ���![]() ����ABC�ڣ���h��ȡֵ��Χ��
����ABC�ڣ���h��ȡֵ��Χ��
��3����PΪ�߶�BC�ϵ�һ���㣨��P�����B,C�غϣ�������P��x��Ĵ��߽���1���е��������ڵ�Q������PQC����ABC����ʱ������PQC�������
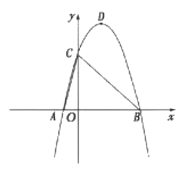
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijҩ�깺��һ������Һ���ƻ�ÿƿ���100Ԫ����������õ���Ч���ƣ�ҩ���������������Һȫ���������ۣ���ÿ�ν��۵İٷ�����ͬ�������������ν��ۺ�ÿƿ�ۼ�Ϊ81Ԫ.
��1����ÿ�ν��۵İٷ���.
��2��������۳��ۣ�ÿƿ��ӯ��100%���ʵ�һ�ν��ۺ���������Һ100ƿ���ڶ��ν��ۺ�������Ҫ���۶���ƿ����������ܳ���5000Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��Rt![]() ABC�У���C��90����AC��10��BC��16������P��ÿ��3����λ���ٶȴӵ�A��ʼ���C�ƶ���ֱ��l����AC�غϵ�λ�ÿ�ʼ������ͬ���ٶ���CB����ƽ���ƶ����ҷֱ���CB��AB�߽���E��F���㣬��P��ֱ��lͬʱ���������˶���ʱ��Ϊt�룬����P�ƶ������C�غ�ʱ����P��ֱ��lͬʱֹͣ�˶������ƶ������У���
ABC�У���C��90����AC��10��BC��16������P��ÿ��3����λ���ٶȴӵ�A��ʼ���C�ƶ���ֱ��l����AC�غϵ�λ�ÿ�ʼ������ͬ���ٶ���CB����ƽ���ƶ����ҷֱ���CB��AB�߽���E��F���㣬��P��ֱ��lͬʱ���������˶���ʱ��Ϊt�룬����P�ƶ������C�غ�ʱ����P��ֱ��lͬʱֹͣ�˶������ƶ������У���![]() PEF�Ƶ�E��ʱ����ת��ʹ�õ�P�Ķ�Ӧ��M����ֱ��l�ϣ���F�Ķ�Ӧ���Ϊ��N������BN����BN��PEʱ��t��ֵΪ_____��
PEF�Ƶ�E��ʱ����ת��ʹ�õ�P�Ķ�Ӧ��M����ֱ��l�ϣ���F�Ķ�Ӧ���Ϊ��N������BN����BN��PEʱ��t��ֵΪ_____��
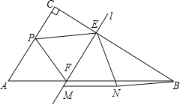
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com