解:(1)4y
2-25=0,
(2y+5)(2y-5)=0,
所以y
1=-

,y
2=

;
(2)(2x+3)
2-36=0;
(2x+3+6)(2x+3-6)=0,
所以x
1=-

,x
2=

;
(3)4(2x+5)
2-1=0;
[2(2x+5)+1][2(2x+5)-1]=0,
所以x
1=-

,x
2=-

;
(4)
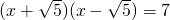
;
x
2-5=7,
x
2=12,
所以x
1=-2

,x
2=2

;
(5)x
2+4x-1=0;
∵a=1,b=4,c=-1,
∴△=16-4×1×(-1)=20,
∴x=
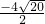
=-2±

,
所以x
1=-2+

,x
2=-2-

;
(6)x
2-3x+2=0;
(x-1)(x-2)=0,
所以x
1=1,x
2=2;
(7)2t
2-7t-4=0;
(t-4)(2t+1)=0,
所以t
1=4,t
2=-

;
(8)(2x-1)
2=(x-2)
2.
2x-1=±(x-2),
即2x-1=x-2,或2x-1=-(x-2),
所以x
1=-1,x
2=1.
分析:(1)运用因式分解法求解;
(2)运用因式分解法求解;
(3)运用因式分解法求解;
(4)先将左边运用平方差公式展开,再移项、合并同类项,运用直接开平方法求解;
(5)运用求根公式法求解;
(6)运用因式分解法求解;
(7)运用因式分解法求解;
(8)运用直接开平方法求解.
点评:本题考查的是解一元二次方程,根据题目的要求和结构特点,选择适当的方法解方程.

 ;
; ,y2=
,y2= ;
; ,x2=
,x2= ;
; ,x2=-
,x2=- ;
; ;
; ,x2=2
,x2=2 ;
;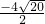 =-2±
=-2± ,
, ,x2=-2-
,x2=-2- ;
; ;
;

 阅读快车系列答案
阅读快车系列答案