
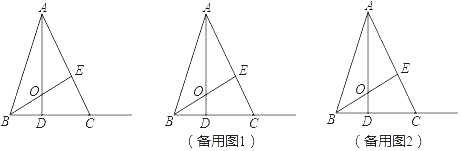
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬BC£½5£¬øßAD”¢BEĻą½»ÓŚµćO£¬BD£½![]() CD£¬ĒŅAE£½BE£®
CD£¬ĒŅAE£½BE£®
£Ø1£©ĒóĻ߶ĪAOµÄ³¤£»
£Ø2£©¶ÆµćP“ÓµćO³ö·¢£¬ŃŲĻ߶ĪOAŅŌĆæĆė1øöµ„Ī»³¤¶ČµÄĖŁ¶ČĻņÖÕµćAŌĖ¶Æ£¬¶ÆµćQ“ÓµćB³ö·¢ŃŲÉäĻßBCŅŌĆæĆė4øöµ„Ī»³¤¶ČµÄĖŁ¶ČŌĖ¶Æ£¬P”¢QĮ½µćĶ¬Ź±³ö·¢£¬µ±µćPµ½“ļAµćŹ±£¬P”¢QĮ½µćĶ¬Ź±Ķ£Ö¹ŌĖ¶Æ£®ÉčµćPµÄŌĖ¶ÆŹ±¼äĪŖtĆė£¬”÷POQµÄĆ껿ĪŖS£¬ĒėÓĆŗ¬tµÄŹ½×Ó±ķŹ¾S£¬²¢Ö±½ÓŠ“³öĻąÓ¦µÄtµÄȔֵ·¶Ī§£»
£Ø3£©ŌŚ£Ø2£©µÄĢõ¼žĻĀ£¬µćFŹĒÖ±ĻßACÉĻµÄŅ»µćĒŅCF£½BO£®ŹĒ·ń“ęŌŚtÖµ£¬Ź¹ŅŌµćB”¢O”¢PĪŖ¶„µćµÄČż½ĒŠĪÓėŅŌµćF”¢C”¢QĪŖ¶„µćµÄČż½ĒŠĪČ«µČ£æČō“ęŌŚ£¬ĒėÖ±½ÓŠ“³ö·ūŗĻĢõ¼žµÄtÖµ£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
”¾“š°ø”æ£Ø1£©AO£½BC£½5£»£Ø2£©¢ŁS£½©2t2+t£Ø0£¼t£¼![]() £©£»¢ŚS£½2t2©t£Ø
£©£»¢ŚS£½2t2©t£Ø![]() £¼t”Ü5£©£»£Ø3£©“ęŌŚ£»t£½1»ņ
£¼t”Ü5£©£»£Ø3£©“ęŌŚ£»t£½1»ņ![]() s£®
s£®
”¾½āĪö”æ
£Ø1£©Ö»ŅŖÖ¤Ć÷”÷AOE”Õ”÷BCE¼“æɽā¾öĪŹĢā£»
£Ø2£©·ÖĮ½ÖÖĒéŠĪĢÖĀŪĒó½ā¼“æÉ¢Łµ±µćQŌŚĻ߶ĪBDÉĻŹ±£¬QD£½2©4t£¬¢Śµ±µćQŌŚÉäĻßDCÉĻŹ±£¬DQ£½4t©2Ź±£»
£Ø3£©·ÖĮ½ÖÖĒéŠĪĒó½ā¼“æÉ¢ŁČēĶ¼2ÖŠ£¬µ±OP£½CQŹ±£¬BOP”Õ”÷FCQ£®¢ŚČēĶ¼3ÖŠ£¬µ±OP£½CQŹ±£¬”÷BOP”Õ”÷FCQ.
½ā£ŗ£Ø1£©ČēĶ¼1ÖŠ£¬
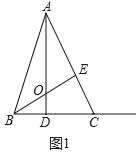
”ßADŹĒøߣ¬
”ą”ĻADC£½90”ć£¬
”ßBEŹĒøߣ¬
”ą”ĻAEB£½”ĻBEC£½90”ć£¬
”ą”ĻEAO+”ĻACD£½90”ć£¬”ĻEBC+”ĻECB£½90”ć£¬
”ą”ĻEAO£½”ĻEBC£¬
ŌŚ”÷AOEŗĶ”÷BCEÖŠ£¬
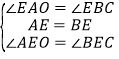 £¬
£¬
”ą”÷AOE”Õ”÷BCE£¬
”ąAO£½BC£½5£®
£Ø2£©”ßBD£½![]() CD£¬BC£½5£¬
CD£¬BC£½5£¬
”ąBD£½2£¬CD£½3£¬
ÓÉĢāŅāOP£½t£¬BQ£½4t£¬
¢Łµ±µćQŌŚĻ߶ĪBDÉĻŹ±£¬QD£½2©4t£¬
”ąS£½![]() t£Ø2©4t£©£½©2t2+t£Ø0£¼t£¼
t£Ø2©4t£©£½©2t2+t£Ø0£¼t£¼![]() £©£®
£©£®
¢Śµ±µćQŌŚÉäĻßDCÉĻŹ±£¬DQ£½4t©2£¬
”ąS£½![]() t£Ø4t©2£©£½2t2©t£Ø
t£Ø4t©2£©£½2t2©t£Ø![]() £¼t”Ü5£©£®
£¼t”Ü5£©£®
£Ø3£©“ęŌŚ£®
¢ŁČēĶ¼2ÖŠ£¬µ±OP£½CQŹ±£¬”ßOB£½CF£¬”ĻPOB£½”ĻFCQ£¬”ą”÷BOP”Õ”÷FCQ£®
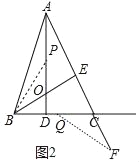
”ąCQ£½OP£¬
”ą5©4tØTt£¬
½āµĆt£½1£¬
¢ŚČēĶ¼3ÖŠ£¬µ±OP£½CQŹ±£¬”ßOB£½CF£¬”ĻPOB£½”ĻFCQ£¬
”ą”÷BOP”Õ”÷FCQ£®

”ąCQ£½OP£¬
”ą4t©5£½t£¬
½āµĆt£½![]() £®
£®
×ŪÉĻĖłŹö£¬t£½1»ņ![]() sŹ±£¬”÷BOPÓė”÷FCQČ«µČ£®
sŹ±£¬”÷BOPÓė”÷FCQČ«µČ£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æijÉĢµźĻśŹŪ![]() Į½ÖÖÉĢĘ·£¬Ć漞µÄŹŪ¼Ū·Ö±šĪŖ
Į½ÖÖÉĢĘ·£¬Ć漞µÄŹŪ¼Ū·Ö±šĪŖ![]() ŌŖ”¢
ŌŖ”¢![]() ŌŖ£¬ĪåŅ»ĘŚ¼ä£¬øĆÉĢµź¾ö¶Ø¶ŌÕāĮ½ÖÖÉĢĘ·½ųŠŠ“ŁĻś»ī¶Æ£¬ČēĶ¼ĖłŹ¾£¬ČōŠ”ŗģ“ņĖćµ½øĆÉĢµź¹ŗĀņ
ŌŖ£¬ĪåŅ»ĘŚ¼ä£¬øĆÉĢµź¾ö¶Ø¶ŌÕāĮ½ÖÖÉĢĘ·½ųŠŠ“ŁĻś»ī¶Æ£¬ČēĶ¼ĖłŹ¾£¬ČōŠ”ŗģ“ņĖćµ½øĆÉĢµź¹ŗĀņ![]() ¼ž
¼ž![]() ÉĢĘ·ŗĶ
ÉĢĘ·ŗĶ![]() ¼ž
¼ž![]() ÉĢĘ·£¬øł¾ŻŅŌÉĻŠÅĻ¢£¬Ēė£ŗ
ÉĢĘ·£¬øł¾ŻŅŌÉĻŠÅĻ¢£¬Ēė£ŗ

£Ø1£©·Ö±šÓĆŗ¬µÄ“śŹżŹ½±ķŹ¾°“ÕÕ·½°øŅ»ŗĶ·½°ø¶žĖłŠčµÄ·ŃÓĆ![]() ŗĶ
ŗĶ![]() £»
£»
£Ø2£©¾Ķ![]() µÄ²»Ķ¬Č”Öµ£¬ĒėĖµĆ÷Ń”ŌńÄĒÖÖ·½°ø¹ŗĀņøüŹµ»Ż£ØĮ½ÖÖÓÅ»Ż·½°ø²»ÄÜĶ¬Ź±ĻķŹÜ£©
µÄ²»Ķ¬Č”Öµ£¬ĒėĖµĆ÷Ń”ŌńÄĒÖÖ·½°ø¹ŗĀņøüŹµ»Ż£ØĮ½ÖÖÓÅ»Ż·½°ø²»ÄÜĶ¬Ź±ĻķŹÜ£©
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼1£¬ ”ŃOŹĒµČ±ßČż½ĒŠĪ ![]() µÄĶā½ÓŌ²£¬
µÄĶā½ÓŌ²£¬ ![]() ŹĒ”ŃOÉĻµÄŅ»øöµć£®
ŹĒ”ŃOÉĻµÄŅ»øöµć£®
£Ø1£©Ōņ ![]() =£»
=£»
£Ø2£©ŹŌÖ¤Ć÷£ŗ ![]() £»
£»
£Ø3£©ČēĶ¼2£¬¹żµć ![]() ×÷”ŃOµÄĒŠĻß½»ÉäĻß
×÷”ŃOµÄĒŠĻß½»ÉäĻß ![]() ÓŚµć
ÓŚµć ![]() £®
£®
¢ŁŹŌÖ¤Ć÷£ŗ ![]() £»
£»
¢ŚČō ![]() £¬Ēó
£¬Ēó ![]() µÄ³¤£®
µÄ³¤£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŗ£ÖŠÓŠŅ»µĘĖžP£¬ĖüµÄÖÜĪ§8ŗ£ĄļÄŚÓŠ°µ½ø£®ŗ£ĀÖŅŌ18ŗ£Ąļ/Ź±µÄĖŁ¶ČÓÉĪ÷Ļņ¶«ŗ½ŠŠ£¬ŌŚA“¦²āµĆµĘĖžPŌŚ±±Ę«¶«60”ć·½ĻņÉĻ£»ŗ½ŠŠ40·ÖÖÓµ½“ļB“¦£¬²āµĆµĘĖžPŌŚ±±Ę«¶«30”ć·½ĻņÉĻ£»Čē¹ūŗ£ĀÖ²»øıäŗ½Ļß¼ĢŠųĻņ¶«ŗ½ŠŠ£¬ÓŠĆ»ÓŠ“„½øµÄĪ£ĻÕ£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æÄ³ÖŠŃ§øÄøļѧɜµÄѧĻ°Ä£Ź½£¬±ä”°ĄĻŹ¦ŅŖѧɜѧĻ°”±ĪŖ”°Ń§Éś×ŌÖ÷ѧĻ°”±£¬ÅąŃųĮĖѧɜ×ŌÖ÷ѧĻ°µÄÄÜĮ¦£®Š”»ŖÓėŠ”Ć÷Ķ¬Ń§¾Ķ”°Äć×īĻ²»¶ÄÄÖÖѧĻ°·½Ź½”±Ė껜µ÷²éĮĖĖūĆĒÖÜĪ§µÄŅ»Š©Ķ¬Ń§£¬øł¾ŻŹÕ¼Æµ½µÄŹż¾Ż»ęÖĘĮĖŅŌĻĀĮ½øö²»ĶźÕūµÄĶ³¼ĘĶ¼£ØČēĶ¼£©£®


Ēėøł¾ŻÉĻĆęĮ½øö²»ĶźÕūµÄĶ³¼ĘĶ¼»Ų“šŅŌĻĀ4øöĪŹĢā£ŗ
£Ø1£©Õā“Ī³éŃłµ÷²éÖŠ£¬¹²µ÷²éĮĖ_____Ćūѧɜ£®
£Ø2£©²¹Č«ĢõŠĪĶ³¼ĘĶ¼ÖŠµÄȱĻī£®
£Ø3£©ŌŚÉČŠĪĶ³¼ĘĶ¼ÖŠ£¬Ń”Ōń½ĢŹ¦“«ŹŚµÄÕ¼_____%£¬Ń”ŌńŠ”×éŗĻ×÷ѧĻ°µÄÕ¼_____%£®
£Ø4£©øł¾Żµ÷²é½į¹ū£¬¹ĄĖćøĆŠ£1800Ćūѧɜ֊“óŌ¼ÓŠ_____ČĖŃ”ŌńŠ”×éŗĻ×÷ѧĻ°Ä£Ź½£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬”ĻC=90”ć£¬ŅŌABÉĻŅ»µćOĪŖŌ²ŠÄ£¬OA³¤ĪŖ°ė¾¶µÄŌ²ÓėBCĻąĒŠÓŚµćD£¬·Ö±š½»AC”¢ABÓŚµćE”¢F£®ČōAC=6£¬AB=10£¬Ōņ”ŃOµÄ°ė¾¶ĪŖ £® 
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ¼ĘĖć£ŗ
(1)![]() ©
©![]() +|
+|![]() ©3|
©3|
(2)x2x4©(©3x2)3
(3)(m+1)(m©3)©(m+2)2+(m+2)(m©2)
(4)20142©2013”Į2015(ÓĆ¹«Ź½¼ĘĖć)
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬Ö±Ļß ![]() ÓėÅ×ĪļĻß
ÓėÅ×ĪļĻß ![]() ½»ÓŚA”¢BĮ½µć£¬µćAŌŚxÖįÉĻ£¬µćBµÄŗį×ų±źĪŖ£8£®
½»ÓŚA”¢BĮ½µć£¬µćAŌŚxÖįÉĻ£¬µćBµÄŗį×ų±źĪŖ£8£®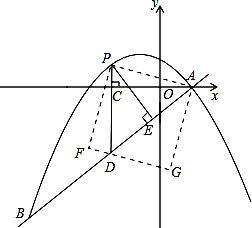
£Ø1£©ĒóøĆÅ×ĪļĻߵĽāĪöŹ½£»
£Ø2£©µćPŹĒÖ±ĻßABÉĻ·½µÄÅ×ĪļĻßÉĻŅ»¶Æµć£Ø²»ÓėµćA”¢BÖŲŗĻ£©£¬¹żµćP×÷xÖįµÄ“¹Ļߣ¬“¹×ćĪŖC£¬½»Ö±ĻßABÓŚµćD£¬×÷PE”ĶABÓŚµćE£®
¢ŁÉč”÷PDEµÄÖܳ¤ĪŖ ![]() £¬µćPµÄŗį×ų±źĪŖ
£¬µćPµÄŗį×ų±źĪŖ ![]() £¬Ēó
£¬Ēó ![]() ¹ŲÓŚ
¹ŲÓŚ ![]() µÄŗÆŹż¹ŲĻµŹ½£¬²¢Ēó³ö
µÄŗÆŹż¹ŲĻµŹ½£¬²¢Ēó³ö ![]() µÄ×ī“óÖµ£»
µÄ×ī“óÖµ£»
¢ŚĮ¬½ÓPA£¬ŅŌPAĪŖ±ß×÷Ķ¼Ź¾Ņ»²ąµÄÕż·½ŠĪAPFG£®Ėę×ŵćPµÄŌĖ¶Æ£¬Õż·½ŠĪµÄ“óŠ””¢Ī»ÖĆŅ²ĖęÖ®øı䣮µ±¶„µćF»ņGĒ”ŗĆĀäŌŚ ![]() ÖįÉĻŹ±£¬Ēó³ö¶ŌÓ¦µćPµÄ×ų±ź£®
ÖįÉĻŹ±£¬Ēó³ö¶ŌÓ¦µćPµÄ×ų±ź£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼1£¬ŌŚRt”÷ABCÖŠ£¬”ĻB=90”ć£¬µćP“ÓµćA³ö·¢£¬ŃŲA”śB”śCŅŌ1cm/sµÄĖŁ¶ČŌĖ¶Æ£®Éč”÷APCµÄĆ껿ĪŖs£Øm£©£¬µćPµÄŌĖ¶ÆŹ±¼äĪŖt£Øs£©£¬±äĮæSÓėtÖ®¼äµÄ¹ŲĻµČēĶ¼2ĖłŹ¾£¬ŌņŌŚŌĖ¶Æ¹ż³ĢÖŠ£¬SµÄ×ī“óÖµŹĒ______£®

²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com