
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{y=x+4.5}\\{\frac{1}{2}y=x+1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{y=x+4.5}\\{\frac{1}{2}y=x-1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{y=4.5-x}\\{\frac{1}{2}y=x+1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{y=x-4.5}\\{\frac{1}{2}y=x-1}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
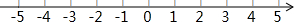 解不等式组$\left\{\begin{array}{l}{\frac{x}{2}>-1①}\\{2x+1≥5(x-1)②}\end{array}\right.$,并把它的解集在如图所示顶点数轴上表示出来.
解不等式组$\left\{\begin{array}{l}{\frac{x}{2}>-1①}\\{2x+1≥5(x-1)②}\end{array}\right.$,并把它的解集在如图所示顶点数轴上表示出来.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 为缓解“停车难”的问题,某单位拟建造地下停车库,建筑设计师提供了该地下车库的设计示意图(如图),按规定,地下车库坡道口上方要张贴限高标志,以便高职停车人车辆能否安全驶入.
为缓解“停车难”的问题,某单位拟建造地下停车库,建筑设计师提供了该地下车库的设计示意图(如图),按规定,地下车库坡道口上方要张贴限高标志,以便高职停车人车辆能否安全驶入.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com