
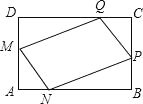
【题目】为了美化环境,学校准备在如图所示的矩形ABCD空地上迸行绿化,规划在中间的一块四边形MNQP上种花,其余的四块三角形上铺设草坪,要求AM=AN=CP=CQ.已知BC=24米,AB=40米,设AN=x米,种花的面积为y1平方米,草坪面积y2平方米.
(1)分别求y1和y2与x之间的函数关系式(不要求写出自变量的取值范围)
(2)当AN的长为多少米时种花的面积为440平方米?
(3)若种花每平方米需200元,铺设草坪每平方米需100元现设计要求种花的面积不大于440平方米,那么学校至少需要准备多少元费用.
【答案】(1)y1=40×24﹣y2=﹣2x2+64x,y2=2x2﹣64x+960;
(2)AN的长为10米或22米时种花的面积为440平方米;
(3)学校至少要准备140000元.
【解析】
试题分析:(1)根据三角形面积公式可得y2的解析式,再用长方形面积减去四个三角形面积,即可得y1的函数解析式;
(2)根据题意知y1=440,即即可得关于x的方程,解方程即可得;
(3)列出总费用的函数解析式,将其配方成顶点式,根据花的面积不大于440平方米可得x的范围,结合此范围根据二次函数性质即可得函数的最大值,从而得解.
试题解析:(1)根据题意,y2=2×![]() xx+2×
xx+2×![]() (40﹣x)(24﹣x)=2x2﹣64x+960,
(40﹣x)(24﹣x)=2x2﹣64x+960,
y1=40×24﹣y2=﹣2x2+64x;
(2)根据题意,知y1=440,即﹣2x2+64x=440,
解得:x1=10,x2=22,
故当AN的长为10米或22米时种花的面积为440平方米;
(3)设总费用为W元,
则W=200(﹣2x2+64x)+100(2x2﹣64x+960)=﹣200(x﹣16)2+147200,
由(2)知当0<x≤10或22≤x≤24时,y1≤440,
在W=﹣200(x﹣16)2+147200中,当x<16时,W随x的增大而增大,当x>16时,W随x的增大而减小,
∴当x=10时,W取得最大值,最大值W=140000,
当x=22时,W取得最大值,最大值W=140000,
∴学校至少要准备140000元.


科目:初中数学 来源: 题型:
【题目】已知x,y互为相反数,m,n互为倒数,且有|a﹣2|=3,试求下面代数式的值:a2﹣(x+y+mn)a+(x+y)2017﹣(﹣mn)2017.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,对于平面内任一点(m,n),规定以下两种变换: ⑴f(m,n)=(m,﹣n),如f(2,1)=(2,﹣1);
⑵g(m,n)=(﹣m,﹣n),如g (2,1)=(﹣2,﹣1)
按照以上变换有:f[g(3,4)]=f(﹣3,﹣4)=(﹣3,4),那么g[f(﹣3,2)]= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一般情况下![]() 不成立,但有些数可以使得它成立,例如:a=b=0.我们称使得
不成立,但有些数可以使得它成立,例如:a=b=0.我们称使得![]() 成立的一对数a,b为“相伴数对”,记为(a,b).
成立的一对数a,b为“相伴数对”,记为(a,b).
(1)若(1,b)是“相伴数对”,求b的值;
(2)写出一个“相伴数对”(a,b),其中a≠0,且a≠1;
(3)若(m,n)是“相伴数对”,求代数式m﹣![]() n﹣[4m﹣2(3n﹣1)]的值.
n﹣[4m﹣2(3n﹣1)]的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有A、B两种商品,买2件A商品和1件B商品用了90元,买3件A商品和2件B商品用了160元.
(1)求A,B两种商品每件各是多少元?
(2)如果小红准备购买A,B两种商品共10件,总费用不超过350元,问小红最多可以买多少件B商品?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com