
【题目】矩形ABCD中,AB=4,AD=3,P,Q是对角线BD上不重合的两点,点P关于直线AD,AB的对称点分别是点E、F,点Q关于直线BC、CD的对称点分别是点G、H.若由点E、F、G、H构成的四边形恰好为菱形,则PQ的长为 .
【答案】2.8
【解析】解:由矩形ABCD中,AB=4,AD=3,可得对角线AC=BD=5.
依题意画出图形,如图所示.
由轴对称性质可知,∠PAF+∠PAE=2∠PAB+2∠PAD=2(∠PAB+∠PAD)=180°,
∴点A在菱形EFGH的边EF上.同理可知,点B、C、D均在菱形EFGH的边上.
∵AP=AE=AF,∴点A为EF中点.同理可知,点C为GH中点.
连接AC,交BD于点O,则有AF=CG,且AF∥CG,
∴四边形ACGF为平行四边形,
∴FG=AC=5,即菱形EFGH的边长等于矩形ABCD的对角线长.
∴EF=FG=5,
∵AP=AE=AF,∴AP= ![]() EF=2.5.
EF=2.5.
∵OA= ![]() AC=2.5,
AC=2.5,
∴AP=AO,即△APO为等腰三角形.
过点A作AN⊥BD交BD于点N,则点N为OP的中点.
由S△ABD= ![]() ABAD=
ABAD= ![]() ACAN,可求得:AN=2.4.
ACAN,可求得:AN=2.4.
在Rt△AON中,由勾股定理得:ON= ![]() =
= ![]() =0.7,
=0.7,
∴OP=2ON=1.4;
同理可求得:OQ=1.4,
∴PQ=OP+OQ=1.4+1.4=2.8.
所以答案是:2.8.


科目:初中数学 来源: 题型:
【题目】如图,已知直线lAC:y=﹣![]() 交x轴、y轴分别为A、C两点,直线BC⊥AC交x轴于点B.
交x轴、y轴分别为A、C两点,直线BC⊥AC交x轴于点B.
(1)求点B的坐标及直线BC的解析式;
(2)将△OBC关于BC边翻折,得到△O′BC,过点O′作直线O′E垂直x轴于点E,F是y轴上一点,P是直线O′E上任意一点,P、Q两点关于x轴对称,当|PA﹣PC|最大时,请求出QF+![]() FC的最小值;
FC的最小值;
(3)若M是直线O′E上一点,且QM=3![]() ,在(2)的条件下,在平面直角坐标系中,是否存在点N,使得以Q、F、M、N四点为顶点的四边形是平行四边形?若存在,请直接写出点N的坐标;若不存在,请说明理由.
,在(2)的条件下,在平面直角坐标系中,是否存在点N,使得以Q、F、M、N四点为顶点的四边形是平行四边形?若存在,请直接写出点N的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对反比例函数 ![]() ,下列说法不正确的是( )
,下列说法不正确的是( )
A.它的图象在第一、三象限
B.点(﹣1,﹣4)在它的图象上
C.当x<0时,y随x的增大而减小
D.当x>0时,y随x的增大而增大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是我国古代计时器“漏壶”的示意图,在壶内盛一定量的水,水从壶底的小孔漏出.壶壁内画有刻度,人们根据壶中水面的位置计时,用x表示时间,y表示壶底到水面的高度,则y与x的函数关系式的图象是( ) 
A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结反思后,和乌龟约定再赛一场.图中的函数图象刻画了“龟兔再次赛跑”的故事(x表示乌龟从起点出发所行的时间,y1表示乌龟所行的路程,y2表示兔子所行的路程).有下列说法:

①“龟兔再次赛跑”的路程为1000米;
②兔子和乌龟同时从起点出发;
③乌龟在途中休息了10分钟;
④兔子在途中750米处追上乌龟.
其中正确的说法是 .(把你认为正确说法的序号都填上)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明为准备体育中考,每天早晨坚持锻炼,某天他慢跑到江边,休息一会后快跑回家,能大致反映小明离家的距离y(m)与时间x(s)的函数关系图象是( )
A.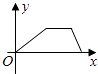
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=(x﹣3)(x+1)与x轴交于A,B两点(点A在点B左侧),与y轴交于点C,点D为顶点.
(1)求点B及点D的坐标.
(2)连结BD,CD,抛物线的对称轴与x轴交于点E.
①若线段BD上一点P,使∠DCP=∠BDE,求点P的坐标.
②若抛物线上一点M,作MN⊥CD,交直线CD于点N,使∠CMN=∠BDE,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“珍重生命,注意安全!”同学们在上下学途中一定要注意骑车安全.小明骑单车上学,当他骑了一段时间,想起要买某本书,于是又折回到刚经过的新华书店,买到书后继续去学校,以下是他本次所用的时间与路程的关系示意图.根据图中提供的信息回答下列问题:

(1)图中自变量是______,因变量是______;
(2)小明家到学校的路程是 米;
(3)小明在书店停留了 分钟;
(4)本次上学途中,小明一共行驶了 米,一共用了 分钟;
(5)我们认为骑单车的速度超过300米/分钟就超越了安全限度.问:在整个上学的途中哪个时间段小明骑车速度最快,速度在安全限度内吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售甲、乙两种品牌的智能手机,这两种手机的进价和售价如下表:
甲 | 乙 | |
进价(元/部) | 4000 | 2500 |
售价(元/部) | 4300 | 3000 |
该商场计划购进两种手机若干部,共需15.5万元,预计全部销售后可获毛利润共2.1万元.
(毛利润=(售价﹣进价)×销售量)
(1)该商场计划购进甲、乙两种手机各多少部?
(2)通过市场调研,该商场决定在原计划的基础上,减少甲种手机的购进数量,增加乙种手机的购进数量.已知乙种手机增加的数量是甲种手机减少的数量的2倍,而且用于购进这两种手机的总资金不超过16万元,该商场怎样进货,使全部销售后获得的毛利润最大?并求出最大毛利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com