
 如图,Rt△OAB在平面直角坐标系中,点A在x轴的正半轴上,点B在y轴的正半轴上,且OA=3,OB=$\sqrt{3}$,边长为$\frac{3\sqrt{3}}{2}$的等边三角形OCD的一边OC在y轴的正半轴上,点D位于第二象限内.若等边三角形OCD以每秒1个单位的速度沿x轴的正方向运动,点D运动到y轴上则停止运动;设点O运动的对应点为点E,ED与y轴的交点为F,CD与y轴和AB的交点分别为H,G,CE与AB的交点为M,设△OCD运动的时间为t秒,△ECD与△OAB重叠部分的面积为S.
如图,Rt△OAB在平面直角坐标系中,点A在x轴的正半轴上,点B在y轴的正半轴上,且OA=3,OB=$\sqrt{3}$,边长为$\frac{3\sqrt{3}}{2}$的等边三角形OCD的一边OC在y轴的正半轴上,点D位于第二象限内.若等边三角形OCD以每秒1个单位的速度沿x轴的正方向运动,点D运动到y轴上则停止运动;设点O运动的对应点为点E,ED与y轴的交点为F,CD与y轴和AB的交点分别为H,G,CE与AB的交点为M,设△OCD运动的时间为t秒,△ECD与△OAB重叠部分的面积为S.分析 (1)如图1中,作DH⊥OC于H.根据等边三角形的性质求出点D的坐标,即可解决问题.
(2)分两种情形讨论①如图3中,当0<t≤$\frac{3}{2}$时,重叠部分是平行四边形EFBM,②如图4中,当$\frac{3}{2}$<t≤$\frac{9}{4}$时,重叠部分是五边形EFHKM.分别计算即可.
(3)当△FEM是等边三角形时,E,F,M,P为顶点的四边形是菱形,分三种情形讨论即可解决问题.
解答 解:(1)如图1中,作DH⊥OC于H.
∵△ODC是等边三角形,OC=DC=DO=$\frac{3\sqrt{3}}{2}$,
∴DH=DC•sin60°=$\frac{9}{4}$,OH=$\frac{1}{2}$OD=$\frac{3\sqrt{3}}{4}$,
∴D(-$\frac{9}{4}$,$\frac{3\sqrt{3}}{4}$),
∵反比例函数y=$\frac{k}{x}$的图象经过点D,
∴k=-$\frac{27\sqrt{3}}{16}$.
(2)如图2中,当直线CD经过点B时.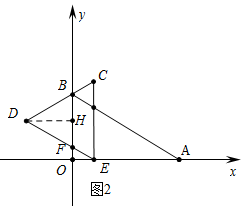
∵DB=DF=BF=$\frac{\sqrt{3}}{2}$,
∴DH=DB•sin60°=$\frac{3}{4}$,OE=$\frac{9}{4}$-$\frac{3}{4}$=$\frac{3}{2}$
①如图3中,当0<t≤$\frac{3}{2}$时,重叠部分是平行四边形EFBM,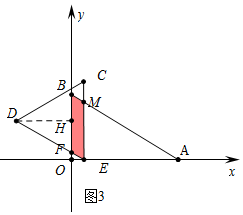
∵直线AB的解析式为y=-$\frac{\sqrt{3}}{3}$x+$\sqrt{3}$,
∵OE=t,
∴ME=-$\frac{\sqrt{3}}{3}$t+$\sqrt{3}$,
∴S=t•(-$\frac{\sqrt{3}}{3}$t+$\sqrt{3}$)=-$\frac{\sqrt{3}}{3}$t2+$\sqrt{3}$t.
②如图4中,当$\frac{3}{2}$<t≤$\frac{9}{4}$时,重叠部分是五边形EFHKM.
S=S△DCE-S△CKM-S△DHF=$\frac{\sqrt{3}}{4}$•($\frac{3\sqrt{3}}{2}$)2-$\frac{\sqrt{3}}{4}$•[$\frac{3\sqrt{3}}{2}$-(-$\frac{\sqrt{3}}{3}$t+$\sqrt{3}$)]2-$\frac{\sqrt{3}}{4}$($\frac{3\sqrt{3}}{2}$-$\frac{2\sqrt{3}}{3}$t)2=-$\frac{5\sqrt{3}}{12}$t2+$\frac{5\sqrt{3}}{4}$t+$\frac{3\sqrt{3}}{2}$,
综上所述,S=$\left\{\begin{array}{l}{-\frac{\sqrt{3}}{3}{t}^{2}+\sqrt{3}t}&{(0<t≤\frac{3}{2})}\\{-\frac{5\sqrt{3}}{12}{t}^{2}+\frac{5\sqrt{3}}{4}t+\frac{3\sqrt{3}}{2}}&{(\frac{3}{2}<t≤\frac{9}{4})}\end{array}\right.$.
(3)如图5中,
当△FEM是等边三角形时,E,F,M,P为顶点的四边形是菱形,
∵EF=EM,
∴$\frac{2\sqrt{3}}{3}$t=-$\frac{\sqrt{3}}{3}$t+$\sqrt{3}$,
∴t=1,
∴OE=1,OF=$\frac{\sqrt{3}}{3}$,
∵四边形EFMP1是菱形,
∴P1(2,$\frac{\sqrt{3}}{3}$),
∵四边形EMP2F是菱形,
∴P2(0,$\sqrt{3}$),
∵四边形EMFP3是菱形,
∴P3(0,-$\frac{\sqrt{3}}{3}$),
综上所述,满足条件的点P坐标为(2,$\frac{\sqrt{3}}{3}$)或(0,$\sqrt{3}$)或(0,-$\frac{\sqrt{3}}{3}$).
点评 本题考查反比例函数综合题、平移变换、多边形面积、等边三角形的性质、菱形的判定和性质等知识,解题的关键是学会分类讨论的思想思考问题,学会利用参数构建方程解决问题,属于中考压轴题.


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:选择题
| A. | 一个有理数的绝对值一定比0大 | |
| B. | 两个数比较大小,绝对值大的反而小 | |
| C. | 相反数等于它本身的数是0 | |
| D. | 若a>0,b<0且|a|>|b|,则a+b<0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,矩形ABCD中,AB=3,BC=4,点P在射线BC上运动,点P和点P′关于BD对称,当P′、P、D三点共线时运动停止,连接DP′、DP.设BP=x.
如图,矩形ABCD中,AB=3,BC=4,点P在射线BC上运动,点P和点P′关于BD对称,当P′、P、D三点共线时运动停止,连接DP′、DP.设BP=x.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-$\frac{2}{3}$)-2=$\frac{4}{9}$ | B. | $\frac{-a+b}{c}$=-$\frac{a+b}{c}$ | ||
| C. | ($\frac{2{a}^{2}}{3b}$)3=$\frac{8{a}^{5}}{9{b}^{3}}$ | D. | $\frac{-a-b}{-a+b}$=$\frac{a+b}{a-b}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,用16m长的铝合金做成一个长方形的窗框.设长方形窗框的横条长度为xm,则长方形窗框的面积为( )
如图,用16m长的铝合金做成一个长方形的窗框.设长方形窗框的横条长度为xm,则长方形窗框的面积为( )| A. | x(16-x)m2 | B. | x(8-x)m2 | C. | x($\frac{16-3x}{2}$)m2 | D. | x($\frac{16-x}{2}$)m2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com