
【题目】如图,已知正方形ABCD,E是AB延长线上一点,F是DC延长线上一点,且满足BF=EF,将线段EF绕点F顺时针旋转90°得FG,过点B作FG的平行线,交DA的延长线于点N,连接NG.

求证:BE=2CF;
试猜想四边形BFGN是什么特殊的四边形,并对你的猜想加以证明.
【答案】详见解析.
【解析】试题分析:(1)过F作FH⊥BE于点H,可证明四边形BCFH为矩形,可得到BH=CF,且H为BE中点,可得BE=2CF;
(2)由条件可证明△ABN≌△HFE,可得BN=EF,可得到BN=GF,且BN∥FG,可证得四边形BFGN为菱形.
试题解析:
证明:过F作FH⊥BE于H点,
在四边形BHFC中,∠BHF=∠CBH=∠BCF=90°,
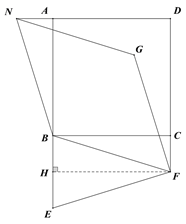
所以四边形BHFC为矩形,
∴CF=BH,
∵BF=EF,FH⊥BE,
∴H为BE中点,
∴BE=2BH,
∴BE=2CF;
猜想:四边形BFGN是菱形.
证明:
∵将线段EF绕点F顺时针旋转90°得FG,
∴EF=GF,∠GFE=90°,
∴∠EFH+∠BFH+∠GFB=90°
∵BN∥FG,
∴∠NBF+∠GFB=180°,
∴∠NBA+∠ABC+∠CBF+∠GFB=180°,
∵∠ABC=90°,
∴∠NBA+∠CBF+∠GFB=180°90°=90°,
由BHFC是矩形可得BC∥HF,∴∠BFH=∠CBF,
∴∠EFH=90°∠GFB∠BFH=90°∠GFB∠CBF=∠NBA,
由BHFC是矩形可得HF=BC,
∵BC=AB,∴HF=AB,
在△ABN和△HFE中, 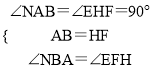 ,
,
∴△ABN≌△HFE,
∴NB=EF,
∵EF=GF,
∴NB=GF,
又∵NB∥GF,
∴NBFG是平行四边形,
∵EF=BF,∴NB=BF,
∴平行四边NBFG是菱形.


科目:初中数学 来源: 题型:
【题目】彩虹服装店用![]() 元购进
元购进![]() 件衬衣,很快全部售完.服装店老板以每件
件衬衣,很快全部售完.服装店老板以每件![]() 元的价格为标准,将超出的记为正数,不足的记为负数,记录如下:
元的价格为标准,将超出的记为正数,不足的记为负数,记录如下:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() (单位:元).他卖完这
(单位:元).他卖完这![]() 件衬衣后是盈利还是亏损?盈利(或亏损)了多少钱?
件衬衣后是盈利还是亏损?盈利(或亏损)了多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某自行车厂计划每天生产![]() 辆自行车,但由于各种原因,实际每天生产量与计划生产量相比有所差异,下表是该厂某一周的实际生产情况(以计划产量为标准,超产记为正数,不足记为负数.单位:辆):
辆自行车,但由于各种原因,实际每天生产量与计划生产量相比有所差异,下表是该厂某一周的实际生产情况(以计划产量为标准,超产记为正数,不足记为负数.单位:辆):
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
与标准产量的差 |
|
|
|
|
|
|
|
(![]() )根据表格,这一周该厂实际生产自行车多少辆?
)根据表格,这一周该厂实际生产自行车多少辆?
(![]() )若该厂实行“每日计件工资制”,每生产一辆自行车可得
)若该厂实行“每日计件工资制”,每生产一辆自行车可得![]() 元,若超额完成任务,则超出部分每辆额外奖励
元,若超额完成任务,则超出部分每辆额外奖励![]() 元;若未完成任务,则每少生产一辆扣
元;若未完成任务,则每少生产一辆扣![]() 元,那么该厂工人这一周的工资总额是多少元?
元,那么该厂工人这一周的工资总额是多少元?
(![]() )若将(
)若将(![]() )中的“每日计件工资制”改为“每周计件工资制”,其他条件不变,在此方式下该厂工人一周的工资总额与“每日计件工资制”相比是减少还是增加了?减少或增加了多少?
)中的“每日计件工资制”改为“每周计件工资制”,其他条件不变,在此方式下该厂工人一周的工资总额与“每日计件工资制”相比是减少还是增加了?减少或增加了多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆慢车和一辆快车沿相同路线从A地到B地,所行驶的路程与时间的函数图象如图所示,下列说法正确的有()个

①快车追上慢车需6小时
②慢车比快车早出发2小时
③快车速度为46km/h
④慢车速度为46km/h
⑤AB两地相距828km
⑥快车14小时到达B地
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形ABCD中,对角线AC与BD交于点O,下列各组条件,其中不能判定四边形ABCD是平行四边形的是( )
A. OA=OC,OB=ODB. OA=OC,AB∥CD
C. AB=CD,OA=OCD. ∠ADB=∠CBD,∠BAD=∠BCD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是明代数学家程大位的《算法统宗》中的一个问题,其大意为:有一群人分银子,如果每人分七两,则剩余四两;如果每人分九两,则还差八两(注:明代时1斤= 16两,故有“半斤八两”这个成语.则下列设未知数列方程正确的序号是____.

①设这群人人数为x,根据题意得7x- 4=9x+ 8;
②设这群人人数为x,根据题意得7x+ 4= 9x一8;
③设所分银子的数量为x两,根据题意得![]() =
=![]()
④设所分银子的数量为x两,根据题意得![]() =
=![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知直线y=x+3与x轴交于点A,与y轴交于点B,将直线在x轴下方的部分沿x轴翻折,得到一个新函数的图象(图中的“V形折线”).

(1)类比研究函数图象的方法,请列举新函数的两条性质,并求新函数的解析式;
(2)如图2,双曲线y=![]() 与新函数的图象交于点C(1,a),点D是线段AC上一动点(不包括端点),过点D作x轴的平行线,与新函数图象交于另一点E,与双曲线交于点P.
与新函数的图象交于点C(1,a),点D是线段AC上一动点(不包括端点),过点D作x轴的平行线,与新函数图象交于另一点E,与双曲线交于点P.
①试求△PAD的面积的最大值;
②探索:在点D运动的过程中,四边形PAEC能否为平行四边形?若能,求出此时点D的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数分别填入相应的集合里.
﹣4,﹣|﹣![]() |,0,
|,0,![]() ,﹣3.14,2019,﹣(+5),+1.88,
,﹣3.14,2019,﹣(+5),+1.88,
(1)正数集合:{ _____…};(2)负数集合:{__________…};
(3)分数集合:{_______…};(4)非负整数集合:{_______…}.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校对七年级全体学生进行了期中测试,并随机抽取了部分学生的测试成绩作为样本进行分析,绘制成了下面的条形图和扇形图(图1和图2均不完整)请根据图中所给的信息,解答下列问题:
(1)求抽取学生的人数,请将表示成绩类别为“中”的条形图补充完整;
(2)求扇形图中表示成绩类别为“优“的扇形所占的百分数;
(3)如果该校七年级共有300人参加期中测试,请估计成绩在“良”及“良”以上的学生人数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com