
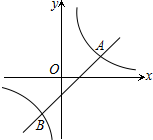
 如图,已知A(4,2)、B(n,-4)是一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象的两个交点
如图,已知A(4,2)、B(n,-4)是一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象的两个交点分析 (1)由点A的坐标利用反比例函数图象上点的坐标特征即可求出m的值;由点B的坐标结合反比例函数图象上点的坐标特征即可得出关于n的一元一次方程,解方程即可求出点B的坐标,再由点A、B的坐标利用待定系数法即可求出一次函数解析;
(2)结合函数图象的上下位置关系结合交点的横坐标,即可得出不等式的解集;
(3)根据反比例函数的性质结合函数图象,即可得出当y1<y2时,t的取值范围.
解答 解:(1)∵点A(4,2)在反比例函数y=$\frac{m}{x}$的图象上,
∴m=4×2=8,
∴反比例函数的解析式为y=$\frac{8}{x}$.
∵点B(n,-4)在反比例函数y=$\frac{8}{x}$的图象上,
∴8=-4n,解得:n=-2,
∴点B的坐标为(-2,-4).
将点A(4,2)、点B(-2,-4)代入到y=kx+b中,
得:$\left\{\begin{array}{l}{2=4k+b}\\{-4=-2k+b}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=1}\\{b=-2}\end{array}\right.$,
∴一次函数的解析式为y=x-2.
(2)观察函数图象,发现:
当x<-2或0<x<4时,反比例函数图象在一次函数图象的上方,
∴不等式$\frac{m}{x}$-kx-b>0的解集为x<-2或0<x<4.
(3)令y=$\frac{8}{x}$中x=1,则y=8,
∴y2=8.
当点M在第三象限内时,y1<0,
显然y1<y2,此时t<0;
当点M的第一象限内时,
∵y=$\frac{8}{x}$中8>0,
∴反比例函数在第一象限内单调递减,
∴若y1<y2,则t>1.
综上可知:当y1<y2时,t的取值范围为t<0或t>1.
点评 本题考查了反比例函数与一次函数的交点问题、反比例函数图象上点的坐标特征以及待定系数法求函数解析式,解题的关键是:(1)求出A、B点的坐标利用待定系数法求函数解析式;(2)利用函数图象的上下位置关系解不等式;(3)根据函数性质找出函数单调性.本题属于中档题,难度不大,但解题过程稍显繁琐,解决该题型题目时,找出点的坐标利用待定系数法求出函数解析式是关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
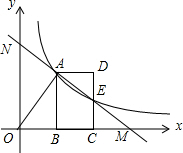 如图,O为原点,反比例函数y=$\frac{k}{x}$(x>0)的图象经过线段OA的端点A,作AB⊥x轴于点B,点A的坐标为(2,3).
如图,O为原点,反比例函数y=$\frac{k}{x}$(x>0)的图象经过线段OA的端点A,作AB⊥x轴于点B,点A的坐标为(2,3).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -4 | B. | -2 | C. | 2 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
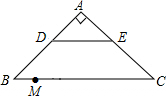 如图,在Rt△ABC中,∠A=90°,AB=AC,BC=20,DE是△ABC的中位线,点M是边BC上一点,BM=3,点N是线段MC上的一个动点,连接DN,ME,DN与ME相交于点O.若△OMN是直角三角形,则DO的长是$\frac{25}{6}$或$\frac{50}{13}$.
如图,在Rt△ABC中,∠A=90°,AB=AC,BC=20,DE是△ABC的中位线,点M是边BC上一点,BM=3,点N是线段MC上的一个动点,连接DN,ME,DN与ME相交于点O.若△OMN是直角三角形,则DO的长是$\frac{25}{6}$或$\frac{50}{13}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,小明想通过测量知道一建筑物AB的高度.他通过测量获得了以下的数据:站在点C处测得建筑物顶端A的仰角为48°,他的眼睛距离地面的高度CD=1.6m,C,B间的距离为12m.请你根据测量获得的数据,计算出建筑物AB的高度是多少?
如图,小明想通过测量知道一建筑物AB的高度.他通过测量获得了以下的数据:站在点C处测得建筑物顶端A的仰角为48°,他的眼睛距离地面的高度CD=1.6m,C,B间的距离为12m.请你根据测量获得的数据,计算出建筑物AB的高度是多少?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
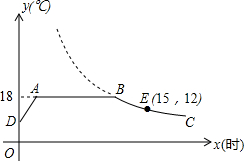 我市某花卉生产基地在气温较低时,用装有恒温系统的温室栽培一种在自然光照且温度为18℃的条件下生长最快的新品种,如图是某天恒温系统从开启到关闭及关闭后,温室内温度y(℃)随时间x(小时)变化的函数图象,其中DA段所满足的表达式为y=5x+13,BC段是反比例函数图象的一部分,点E是BC段上一点.请根据图中信息解答下列问题:
我市某花卉生产基地在气温较低时,用装有恒温系统的温室栽培一种在自然光照且温度为18℃的条件下生长最快的新品种,如图是某天恒温系统从开启到关闭及关闭后,温室内温度y(℃)随时间x(小时)变化的函数图象,其中DA段所满足的表达式为y=5x+13,BC段是反比例函数图象的一部分,点E是BC段上一点.请根据图中信息解答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com