
【题目】如图,△ABC的三条角平分线相交于点I,过点I作DI⊥IC,交AC于点D.
(1)如图①,求证:∠AIB=∠ADI;
(2)如图②,延长BI,交外角∠ACE的平分线于点F.
①判断DI与CF的位置关系,并说明理由;
②若∠BAC=70°,求∠F的度数.


【答案】(1)证明见解析;(2)解:①结论:DI∥CF,②35°.
【解析】(1)只要证明∠AIB=90°+![]() ∠ACB,∠ADI=90°+
∠ACB,∠ADI=90°+![]() ∠ACB即可;
∠ACB即可;
(2)①只要证明∠IDC=∠DCF即可;
②首先求出∠ACE-∠ABC=∠BAC=70°,再证明∠F=![]() ∠ACE-
∠ACE-![]() ∠ABC=
∠ABC=![]() (∠ACE-∠ABC)即可解决问题;
(∠ACE-∠ABC)即可解决问题;
(1)证明:∵AI,BI分别平分∠BAC,∠ABC,
∴∠BAI=![]() ∠BAC,∠ABI=
∠BAC,∠ABI=![]() ∠ABC,
∠ABC,
∴∠BAI+∠ABI=![]() (∠BAC+∠ABC)=
(∠BAC+∠ABC)=![]() (180°-∠ACB)=90°-
(180°-∠ACB)=90°-![]() ∠ACB.
∠ACB.
在△ABI中,∠AIB=180°-(∠BAI+∠ABI)=180°-(90°-![]() ∠ACB)=90°+
∠ACB)=90°+![]() ∠ACB.
∠ACB.
∵CI平分∠ACB,∴∠DCI=![]() ∠ACB.∵DI⊥IC,
∠ACB.∵DI⊥IC,
∴∠DIC=90°,∴∠ADI=∠DIC+∠DCI=90°+![]() ∠ACB.
∠ACB.
∴∠AIB=∠ADI.
(2)解:①结论:DI∥CF.
理由:∵∠IDC=90°-∠DCI=90°-![]() ∠ACB,CF平分∠ACE,
∠ACB,CF平分∠ACE,
∴∠ACF=![]() ∠ACE=
∠ACE=![]() (180°-∠ACB)=90°-
(180°-∠ACB)=90°-![]() ∠ACB,∴∠IDC=∠ACF,∴DI∥CF.
∠ACB,∴∠IDC=∠ACF,∴DI∥CF.
②∵∠ACE=∠ABC+∠BAC,∴∠ACE-∠ABC=∠BAC=70°.
∵∠FCE=∠FBC+∠F,∴∠F=∠FCE-∠FBC.
∵∠FCE=![]() ∠ACE,∠FBC=
∠ACE,∠FBC=![]() ∠ABC,
∠ABC,
∴∠F=![]() ∠ACE-
∠ACE-![]() ∠ABC=
∠ABC=![]() (∠ACE-∠ABC)=35°.
(∠ACE-∠ABC)=35°.


 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:
【题目】Rt△ABC中,∠C=90°,点D、E分别是△ABC边AC、BC上的点,点P是一动点.令∠PDA=∠1,∠PEB=∠2,∠DPE=∠α.
(1)若点P在线段AB上,如图(1)所示,且∠α=50°,则∠1+∠2= °;
(2)若点P在边AB上运动,如图(2)所示,则∠α、∠1、∠2之间的关系为: ;
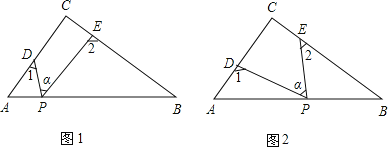
(3)若点P运动到边AB的延长线上,如图(3)所示,则∠α、∠1、∠2之间有何关系?猜想并说明理由.
(4)若点P运动到△ABC形外,如图(4)所示,则∠α、∠1、∠2之间的关系为: .
查看答案和解析>>
科目:初中数学 来源: 题型:
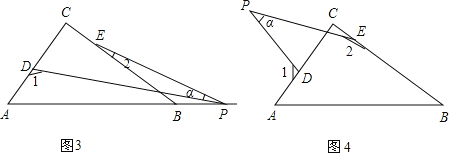
【题目】如图(1)所示,△ABC中,∠ABC,∠ACB的平分线交于点O,求证:∠BOC=90+![]() ∠A.
∠A.
变式1:如图(2)所示,∠ABC,∠ACD的平分线交于点O,求证:∠BOC=![]() ∠A.
∠A.
变式2:如图(3)所示,∠CBD,∠BCE的平分线交于点O,求证:∠BOC=90-![]() ∠A.
∠A.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知直线y= ![]() x+2与x轴交于点A,与y轴交于点C,抛物线y=ax2+4ax+b经过A.C两点,且与x轴交于另一点B.
x+2与x轴交于点A,与y轴交于点C,抛物线y=ax2+4ax+b经过A.C两点,且与x轴交于另一点B.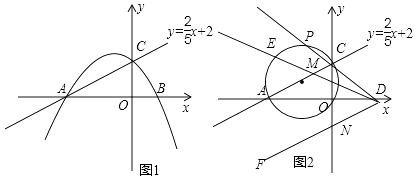
(1)求抛物线的解析式;
(2)若点Q在抛物线上,且△AQC与△BQC面积相等,求点Q的坐标;
(3)如图2,P为△AOC外接圆上弧ACO的中点,直线PC交x轴于点D,∠EDF=∠ACO,当∠EDF绕点D旋转时,DE交直线AC于点M,DF交y轴负半轴于点N.请你探究:CN﹣CM的值是否发生变化?若不变,求出其值;若变化,求出变化范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=BC,点D,E分别是边AB,AC的中点,延长DE至点F,使EF=DE,则四边形ADCF一定是( ) 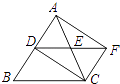
A.矩形
B.菱形
C.正方形
D.梯形
查看答案和解析>>
科目:初中数学 来源: 题型:
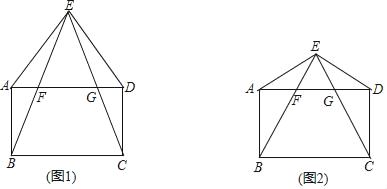
【题目】已知:点E为矩形ABCD外一点,连接AE,DE,且AE=DE,连接EB,EC分别与AD相交于点F,G.
(1)如图1,求证:∠ABE=∠DCE;
(2)如图2,若△BCE是等边三角形,且AE=AB,在不添加任何辅助线的情况下,请直接写出图2中四对全等的钝角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个多位自然数的任意两个相邻数位上,右边数位上的数总比左边数位上数大1,那么我们把这样的自然数叫做“相连数”.例如:234,4567,56789,…都是“相连数”.
(1)请直接写出最大的两位“相连数”与最小的三位“相连数”,并求它们的差.
(2)若某个“相连数”恰好等于其个位数的469倍,求这个“相连数”.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某项针对18﹣35岁的青年人每天发微博数量的调查中,设一个人的“日均发微博条数”为m,规定:当0≤m<5时为A级,5≤m<10时为B级,10≤m<15时为C级,m≥15时为D级.现随机抽取部分符合年龄条件的青年人开展每人“日均发微博条数”的调查,制作图表如下: 18﹣35岁青年人日均发微博条数统计表
m | 频数 | 百分数 |
A级(0≤m<5) | 90 | 0.3 |
B级(5≤m<10) | 120 | a |
C级(10≤m<15) | b | 0.2 |
D级(m≥15) | 30 | 0.1 |
请你根据以上信息解答下列问题:
(1)求a,b;
(2)补全频数分布直方图.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】三角板是学习数学的重要工具,将一副三角板中的两块直角三角板的直角顶点![]() 按如图方式叠放在一起,当
按如图方式叠放在一起,当![]() 且点
且点![]() 在直线
在直线![]() 的上方时,解决下列问题:(友情提示:
的上方时,解决下列问题:(友情提示:![]() ,
,![]() ,
,![]() .
.

(1)①若![]() ,则
,则![]() 的度数为 ;
的度数为 ;
②若![]() ,则
,则![]() 的度数为 ;
的度数为 ;
(2)由(1)猜想![]() 与
与![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
(3)这两块三角板是否存在一组边互相平行?若存在,请直接写出![]() 的角度所有可能的值(不必说明理由);若不存在,请说明理由.
的角度所有可能的值(不必说明理由);若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com