
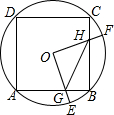
 如图,边长为4的正方形ABCD内接于点O,点E是$\widehat{AB}$上的一动点(不与A,B重合),点F是$\widehat{BC}$上的一点,连接OE,OF,分别与AB,BC交于点G,H,且∠EOF=90°,有以下结论:
如图,边长为4的正方形ABCD内接于点O,点E是$\widehat{AB}$上的一动点(不与A,B重合),点F是$\widehat{BC}$上的一点,连接OE,OF,分别与AB,BC交于点G,H,且∠EOF=90°,有以下结论:| A. | ①③④ | B. | ①②③ | C. | ①② | D. | ③④ |
分析 如图所示,连接OC、OB、CF、BE.
①正确.先证明$\widehat{BE}$=$\widehat{CF}$,由$\widehat{AB}$=$\widehat{BC}$即可证明结论;
②正确.只要证明△BOG≌△COH即可解决问题;
③错误.只要证明S四边形OGBH=S△BOC=$\frac{1}{4}$S正方形ABCD=定值即可;
④错误.当OH⊥BC时,OH的值最小,即△OHG的周长最小,此时OG=OH=2,GH=2$\sqrt{2}$,推出△OGH的周长的最小值为4+2$\sqrt{2}$;
解答 解:如图所示,连接OC、OB、CF、BE.
∵∠BOE+∠BOF=90°,∠COF+∠BOF=90°,
∴∠BOE=∠COF,
∴$\widehat{BE}$=$\widehat{CF}$,
∵$\widehat{AB}$=$\widehat{CB}$,
∴$\widehat{AE}$=$\widehat{BF}$,故①正确,
在△BOG与△COH中,
$\left\{\begin{array}{l}{∠BOG=∠COH}\\{OC=OB}\\{∠OBG=∠OCH=45°}\end{array}\right.$,
∴△BOG≌△COH,
∴OG=OH,∵∠HOG=90°
∴△OGH是等腰直角三角形,②正确,
∴S△OBG=S△OCH,
∴S四边形OGBH=S△BOC=$\frac{1}{4}$S正方形ABCD=定值,故③错误,
∵△OGH是等腰直角三角形,
∴当OH⊥BC时,OH的值最小,即△OHG的周长最小,此时OG=OH=2,GH=2$\sqrt{2}$,
∴△OGH的周长的最小值为4+2$\sqrt{2}$,故④错误.
∴①②正确,
故选C.
点评 本题考查圆综合题、正方形的性质、全等三角形的判定和性质、等腰直角三角形的判定和性质、四边形的面积等知识,解题的关键是灵活运用所学知识解决问题,学会添加常用辅助线.构造全等三角形解决问题,学会利用垂线段最短,解决最值问题,属于中考常考题型.


 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:初中数学 来源: 题型:解答题
| 品名 | 苹果 | 桔子 |
| 批发价(元/千克) | 8.8 | 6.4 |
| 零售价(元/千克) | 14.4 | 10.4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | “随机掷一枚硬币,正面一定朝上”是必然事件 | |
| B. | 数据2,2,3,3,8的众数是8 | |
| C. | 某次抽奖活动获奖的概率为$\frac{1}{60}$,说明每买60张奖券一定有一次中奖 | |
| D. | 某地区有400万电视观众,要想了解他们对新闻、体育、动画、娱乐、戏曲五类节目的喜爱情况,宜采用抽样调查 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com