练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    17．用反证法证明：在四边形中，至少有一个内角大于或等于90°，应先假设（　　）
    A．四边形中每一个内角都小于90°
    B．四边形中最多有一个内角不小于90°
    C．四边形中每一个内角都大于90°
    D．四边形中有一个内角大于90°

    分析 至少有一个角不小于90°的反面是每个角都小于90°，据此即可假设．

    解答 解：用反证法证明：在四边形中，至少有一个角不小于90°，
    应先假设：四边形中的每个角都小于90°．
    故选：A．

    点评 此题考查了反证法，解此题关键要懂得反证法的意义及步骤．在假设结论不成立时要注意考虑结论的反面所有可能的情况，如果只有一种，那么否定一种就可以了，如果有多种情况，则必须一一否定．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    7．先化简，再求值：[（5x+4y）2-4y（5x+4y）]÷（-5x），其中x，y满足：x2-2x+y2+6y+10=0．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    8．请写出一个多项式，含有字母a，并能够在有理数范围内用平方差公式进行因式分解，此多项式可以是a2-4（答案不唯一）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    5．二次函数y=x2-2x+m的图象与x轴的一个交点的坐标是（-1，0），则图象与x轴的另一个交点的坐标是（3，0）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    12．如图，菱形ABCD中，对角线AC，BD相交于点O，H为AD边中点，菱形ABCD的周长为8，则OH的长等于1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

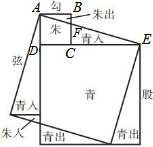    2．魏晋时期，伟大数学家刘徽利用如图通过“以盈补虚，出入相补”的方法，即“勾自乘为朱方，股自乘为青方，令出入相补，各从其类”证明了勾股定理，若图中BF=2，CF=4，则AE的长为6$\sqrt{10}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    9．已知一元二次方程x2-4x+3=0的两根x1、x2，则x12-4x1+x1x2=0．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    6．下列命题是假命题的是（　　）
    A．平行四边形的对角线互相平分B．平行四边形的对角相等
    C．平行四边形是轴对称图形D．平行四边形是中心对称图形

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    7．已知一元二次方程2x2-5x+1=0的两个根为x1，x2，下列结论正确的是（　　）
    A．x1+x2=-$\frac{5}{2}$B．x1•x2=1C．x1，x2都是有理数D．x1，x2都是正数

    查看答案和解析>>

    同步练习册答案