
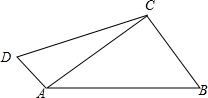
 已知:如图,四边形ABCD中,∠ACB=90°,AB=15,BC=9,AD=5,DC=13.求证:△ACD是直角三角形.
已知:如图,四边形ABCD中,∠ACB=90°,AB=15,BC=9,AD=5,DC=13.求证:△ACD是直角三角形.  天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
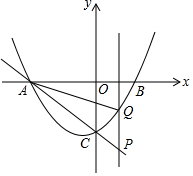 已知抛物线y=$\frac{1}{4}$x2+$\frac{1}{4}$x-3交x轴于A,B两点,交y轴于点C,点P是直线AC上的一个动点,过点P作PQ⊥x轴,交抛物线于点Q,连结CQ.设点P的横坐标为m.
已知抛物线y=$\frac{1}{4}$x2+$\frac{1}{4}$x-3交x轴于A,B两点,交y轴于点C,点P是直线AC上的一个动点,过点P作PQ⊥x轴,交抛物线于点Q,连结CQ.设点P的横坐标为m.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在△ABC中,AD⊥BC,垂足为D,E为AC上一点,BE交AD于点F,且BF=AC,FD=CD,AD=4,则AB=4$\sqrt{2}$.
如图,在△ABC中,AD⊥BC,垂足为D,E为AC上一点,BE交AD于点F,且BF=AC,FD=CD,AD=4,则AB=4$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
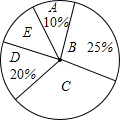 近年来,中学生的身体素质普遍下降,某校为了提高本校学生的身体素质,落实教育部门“在校学生每天体育锻炼时间不少于1小时”的文件精神,对部分学生的每天体育锻炼时间进行了调查统计.以下是本次调查结果的统计表和统计扇形图.
近年来,中学生的身体素质普遍下降,某校为了提高本校学生的身体素质,落实教育部门“在校学生每天体育锻炼时间不少于1小时”的文件精神,对部分学生的每天体育锻炼时间进行了调查统计.以下是本次调查结果的统计表和统计扇形图.| 组别 | A | B | C | D | E |
| 时间t(分钟) | t<40 | 40≤t<60 | 60≤t<80 | 80≤t<100 | t≥100 |
| 人数 | 12 | 30 | a | 24 | 12 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com