
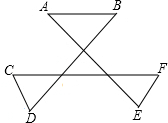
 如图,求∠A+∠B+∠C+∠D+∠E+∠F的度数.
如图,求∠A+∠B+∠C+∠D+∠E+∠F的度数.  第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图是某沿江地区交通平面图,为了加快经济发展,该地区拟修建一条连接M,O,Q三个城市的沿江高速公路,已知该沿江高速公路的建设成本是5000万元/km,该沿江高速公路的造价预计是多少?
如图是某沿江地区交通平面图,为了加快经济发展,该地区拟修建一条连接M,O,Q三个城市的沿江高速公路,已知该沿江高速公路的建设成本是5000万元/km,该沿江高速公路的造价预计是多少?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com