
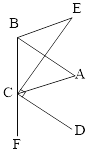
【题目】如图所示,已知BA平分∠EBC, CD平分∠ACF,且![]() ∥CD,
∥CD,
(1)试判断AC与BE的位置关系,并说明理由;
(2)若DC⊥EC于C, 猜想∠E与∠FCD之间的关系,并推理判断你的猜想。
【答案】(1)AC∥BE.理由见解析;(2)∠E与∠FCD互余,理由见解析.
【解析】试题分析:(1)由AB∥CD得到∠ABC=∠DCF,再由BA平分∠EBC, CD平分∠ACF得到∠EBC=2∠ABC,∠ACF=2∠DCF,即可得∠EBC=∠ACF,根据同位角相等得出AC∥BE;
(2)由AC∥BE得到∠E=∠ACE,再由CD平分∠ACF得到∠ACD=∠FCD和DC⊥EC,得到∠ACE+∠ACD=90°,可得出∠E+∠FCD=90°,即∠E与∠FCD互余.
试题解析:
(1)AC∥BE .理由如下:
因为AB∥CD,
所以∠ABC=∠DCF
因为BA平分∠EBC, CD平分∠ACF
所以∠EBC=2∠ABC,∠ACF=2∠DCF
所以∠EBC=∠ACF
所以AC∥BE
(2)∠E与∠FCD互余
因为AC∥BE,所以∠E=∠ACE
因为CD平分∠ACF,所以∠ACD=∠FCD
又因为DC⊥EC,所以∠ACE+∠ACD=90°
所以∠E+∠FCD=90°
即∠E与∠FCD互余


科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=5cm,BC=3cm,AC=4cm,若动点P从点C开始,按C→A→B的路径运动,且速度为每秒2cm,设出发的时间为t秒
(1)请判断△ABC的形状,说明理由.
(2)当t= 时,△BCP是以BC为腰的等腰三角形.
(3)另有一点Q,从点C开始,按C→B→A→C的路径运动,且速度为每秒1cm,若P、Q两点同时出发,当P、Q中有一点到达终点时,另一点也停止运动.当t为何值时,P、Q两点之间的距离为![]() ?
?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的正方形网格中,△ABC 的顶点均在格点上,请在所给直角坐标系中按要求画图和解答下列问题:
(1)以A点为旋转中心,将△ABC绕点A顺时针旋转90°得△AB1C1,画出△AB1C1.
(2)作出△ABC关于坐标原点O成中心对称的△A2B2C2.
(3)作出点C关于x轴的对称点P. 若点P向右平移x个单位长度后落在△A2B2C2的内部(不含落在△A2B2C2的边上),请直接写出x的取值范围..
(提醒:每个小正方形边长为1个单位长度)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了城市绿化建设,某中学初三(2)班计划组织部分同学义务植树180棵,由于同学们参与的积极性很高,实际参加植树活动的人数比原计划增加了![]() ,结果每人比原计划少栽了2棵树,问实际有多少人参加了这次植树活动?
,结果每人比原计划少栽了2棵树,问实际有多少人参加了这次植树活动?
(1)小明设原计划有![]() 人参加植树活动,请你完成他的求解过程;
人参加植树活动,请你完成他的求解过程;
(2)小红设原计划每人栽![]() 棵树,则由题意可得方程为: .(不需要求解)
棵树,则由题意可得方程为: .(不需要求解)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的三个顶点的坐标分别为A(-3,5),B(-3,0),C(2,0),将△ABC绕点B顺时针旋转一定的角度后得到△DBE,且使点D落在y轴上,与此同时顶点E恰好落在y=![]() 的图象上,则k的值为( )
的图象上,则k的值为( )
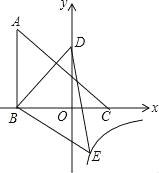
A.-3 B.-4 C.-5 D.-3![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com