
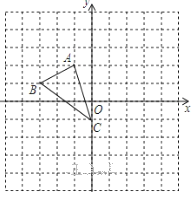
【题目】△ABC与△A′B′C′在平面直角坐标系中的位置如图所示.
(1)分别写出下列各点的坐标:A′________;B′________;C′________;
(2)说明△A′B′C′由△ABC经过怎样的平移得到;
(3)若点P(a,b)是△ABC内部一点,则平移后△A′B′C′内的对应点P′的坐标为________;
(4)求△ABC的面积.

【答案】(1)(-3,1),(-2,-2),(-1,-1);(2)先向左平移4个单位,再向下平移2个单位;(3)(![]() -4,b-2);(4)2
-4,b-2);(4)2
【解析】
(1)直接根据已知图形得出各点坐标即可;
(2)利用对应点的位置关系进一步得出平移规律即可;
(3)利用(2)中的平移规律进一步分析即可得出答案;
(4)利用△ABC所在矩形的面积减去周围的三角形的面积进一步计算即可.
(1)由已知图形可得:A′、B′、C′三点的坐标分别为:(-3,1),(-2,-2),(-1,-1),
故答案为:(-3,1),(-2,-2),(-1,-1);
(2)由题意得可知:A′(-3,1),A(1,3),
∴△ABC先向左平移4个单位,再向下平移2个单位得到△A′B′C′;
(3)由(2)可得:△ABC先向左平移4个单位,再向下平移2个单位得到△A′B′C′,
∴P′的坐标为:(![]() -4,b-2);
-4,b-2);
(4)△ABC的面积=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,有一块直角三角形纸片,两直角边AB=6,BC=8,将△ABC折叠,使AB落在斜边AC上,折痕为AD,则BD的长为( )

A. 6B. 5C. 4D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系网格中,△ABC的顶点都在格点上,点C坐标(0,-1).
![]() 作出△ABC 关于原点对称的△A1B1C1,并写出点A1的坐标;
作出△ABC 关于原点对称的△A1B1C1,并写出点A1的坐标;
![]() 把△ABC 绕点C逆时针旋转90°,得△A2B2C2,画出△A2B2C2,并写出点A2的坐标;
把△ABC 绕点C逆时针旋转90°,得△A2B2C2,画出△A2B2C2,并写出点A2的坐标;
(3)直接写出△A2B2C2的面积
查看答案和解析>>
科目:初中数学 来源: 题型:
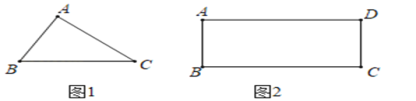
【题目】(1)如图1,已知△ABC,试确定一点D,使得以A,B,C,D为顶点的四边形为平行四边形,请画出这个平行四边形;
(2)如图2,在矩形ABCD中,AB=4,BC=10,若要在该矩形中作出一个面积最大的△BPC,且使∠BPC=90°,求满足条件的点P到点A的距离;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BD是角平分线,且∠ACB=60°,∠ADB=97°,
(1)求∠A
(2) 在图中画出△ABC边AB上的高CE.并求出∠ACE的度数.
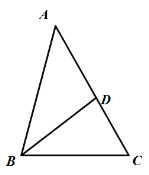
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解我县中学生参加“科普知识”竞赛成绩的情况,随机抽查了部分参赛学生的成绩,整理并制作出如下的统计表和统计图,如图所示.请根据图表信息解答下列问题.
组别 | 分数段(分) | 频数 | 百分率(%) |
A组 | 60≤x<70 | 30 | 10 |
B组 | 70≤x<80 | 90 | n |
C组 | 80≤x<90 | m | 40 |
D组 | 90≤x<100 | 60 | 20 |
(1)样本容量a= ,表中m= ,n= ;
(2)补全频数分布直方图;
(3)若成绩在80分以上(包括80分)为“优”等,请你估计我县参加“科普知识”竞赛的1.5万名学生中成绩是“优”等的约有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察后填空:①(x﹣1)(x+1)=x2﹣1; ②(x﹣1)(x2+x+1)=x3﹣1; ③(x﹣1)(x3+x2+x+1)=x4﹣1.
(1)填空:(x﹣1)(x99+x98+x97+…+x+1)= .
(2)请利用上面的结论计算:
①(﹣2)50+(﹣2)49+(﹣2)48+…+(﹣2)+1; ②若x3+x2+x+1=0,求x2016的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的顶点坐标分别为A(﹣6,0),B(4,0),C(0,8),把△ABC沿直线BC翻折,点A的对应点为D,抛物线y=ax2﹣10ax+c经过点C,顶点M在直线BC上.

(1)证明四边形ABCD是菱形,并求点D的坐标;
(2)求抛物线的对称轴和函数表达式;
(3)在抛物线上是否存在点P,使得△PBD与△PCD的面积相等?若存在,直接写出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com