
【题目】设A(﹣2,y1),B(1,y2),C(2,y3)是抛物线y=﹣(x+1)2+1上的三点,则y1 , y2 , y3的大小关系为 .
科目:初中数学 来源: 题型:
【题目】如图,直角三角板ABC的斜边AB=12cm,∠A=30°,将三角板ABC绕点C顺时针旋转90°至三角板A′B′C′的位置后,再沿CB方向向左平移,使点B′落在原三角板ABC的斜边AB上,则三角板A′B′C′平移的距离为( )
A.6cm
B.(6﹣2![]() )cm
)cm
C.3cm
D.(4![]() ﹣6)cm
﹣6)cm
查看答案和解析>>
科目:初中数学 来源: 题型:
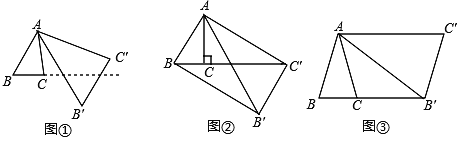
【题目】将△ABC绕点A按逆时针方向旋转θ度,并使各边长变为原来的n倍,得△AB′C′ ,如图①所示,∠BAB′ =θ, ![]() ,我们将这种变换记为[θ,n] .
,我们将这种变换记为[θ,n] .
(1)如图①,对△ABC作变换[60°,![]() ]得到△AB′C′ ,则
]得到△AB′C′ ,则![]() :
:![]() = ;直线BC与直线B′C′所夹的锐角为 度;
= ;直线BC与直线B′C′所夹的锐角为 度;
(2)如图②,△ABC中,∠BAC=30°,∠ACB=90°,对△ABC作变换[θ,n]得到△AB′C′,使点B、C、![]() 在同一直线上,且四边形ABB′C′为矩形,求θ和n的值;
在同一直线上,且四边形ABB′C′为矩形,求θ和n的值;
(3)如图③,△ABC中,AB=AC,∠BAC=36°,BC=1,对△ABC作变换[θ,n]得到△AB′C′,使点B、C、B′在同一直线上,且四边形ABB′C′为平行四边形,求θ和n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,桌面内,直线l上摆放着两块大小相同的直角三角板,它们中较大锐角的度数为60°.将△ECD沿直线l向左平移到图的位置,使E点落在AB上,即点E′,点P为AC与E′D′的交点.
(1)求∠CPD′的度数;
(2)求证:AB⊥E′D′.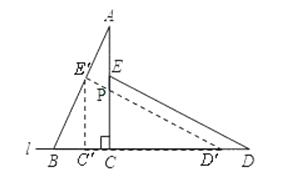
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】三角形的外心是( )
A. 三角形三条边上中线的交点B. 三角形三条边上高线的交点
C. 三角形三条边垂直平分线的交点D. 三角形三条内角平分线的交点
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com