

���� ��1������D��DD���AB���D�䣬����C��CC���AB���C�䣬֤��������ȫ�ȣ��ó�AD��ij��ȣ��ɽǵ�����ֵ�ɵó���A��ֵ��
��2���غϲ��ֵ�������ɷ�����������ǣ�����t��ȡֵ��ͬ���������ۣ�
��3��Ѱ��3���Ƿֱ�Ϊֱ�ǵ���������ݱ߽ǹ�ϵ���ҳ�ʱ��t��ֵ��
��� �⣺��1������D��DD���AB���D�䣬����C��CC���AB���C�䣬��ͼ1��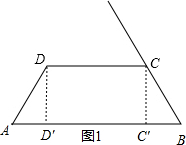
��ABCD��������
���A=��B��AD=BC��
�ڡ�ADD��͡�BCC���У���$\left\{\begin{array}{l}{��A=��B}\\{��AD��D=��BC��C=90��}\\{AD=BC}\end{array}\right.$��
���ADD��ա�BCC�䣨AAS����
��AD��=BC�䣬
��AD��=��AB-CD����2=��10-6����2=2��
��cos��A=$\frac{AD��}{AD}$=$\frac{2}{4}$=$\frac{1}{2}$��
���A=60�㣮
�ʴ�Ϊ��60��
��2����B��Ķ�Ӧ��ΪB�䣬�ɷ�ת�����Կ�֪��PB=PB�䣬
�֡ߡ�B=��A=60�㣬
���BPB��Ϊ�ȱ������Σ�
���BPB��=60��=��A��PB=BB��=PB��
��AD��PB�䣬
�Ӷ���֪���Ϸ��غ�ͼ��ֻ�����������
�ٵ�B�����߶�BC�ϣ���ͼ2��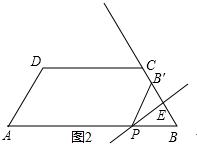
��ʱPB=BB���BC����2t��4�����t��2��
�ߡ�BPB��Ϊ�ȱ������Σ���PE��BB�䣬
��PE=$\frac{\sqrt{3}}{2}$PB=$\sqrt{3}$t��BE=$\frac{1}{2}$PB=t��
�������غϵ����S=$\frac{1}{2}$•PE•BE=$\frac{\sqrt{3}}{2}$t2��
�ڵ�B����BC���ӳ����ϣ���E���߶�BC�ϣ���ͼ3����PB����CD�Ľ���ΪO��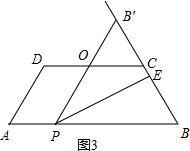
��ʱ��BC��PB��2BC����4��2t��8�����2��t��4��
�ߡ�BPB��Ϊ�ȱ������Σ���CD��AB���������µ�ƽ�У���
���B��OCΪ�ȱ������Σ�
��PE=$\frac{\sqrt{3}}{2}$PB=$\sqrt{3}$t��BE=$\frac{1}{2}$PB=t��B��C=BB��-BC=2t-4��
�������غϵ����S=$\frac{1}{2}$PE•BE-$\frac{1}{2}$��$\frac{1}{2}$B��C��$\frac{\sqrt{3}}{2}$B��C=2$\sqrt{3}$t-2$\sqrt{3}$��
�۵�E���߶�BE���ӳ����ϣ���ͼ4����PB����CD�Ľ���ΪO��PE��CD�Ľ���ΪO�䣬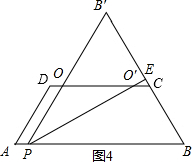
��ʱ��2BC��PB��AB����8��2t��10�����4��t��5��
ͬ����ȣ����غϵ������Ҫ��һ����ECO�䣬
��CD��AB��
���ECO��ס�EBP��
�֡�BE=t��CE=BE-BC=t-4��PE=$\sqrt{3}$t��
��O��E=$\frac{CE}{BE}$•PE=$\sqrt{3}$t-4$\sqrt{3}$��
�������غϵ����S=2$\sqrt{3}$t-2$\sqrt{3}$+$\frac{1}{2}$•O��E•CE=$\frac{\sqrt{3}}{2}$t2-2$\sqrt{3}$t+6$\sqrt{3}$��
�ۺϢ٢ڢۿɵã��������غϵ����S=$\left\{\begin{array}{l}{\frac{\sqrt{3}}{2}{t}^{2}��0��t��2��}\\{2\sqrt{3}t-2\sqrt{3}��2��2��4��}\\{\frac{\sqrt{3}}{2}{t}^{2}-2\sqrt{3}t+6\sqrt{3}��4��t��5��}\end{array}\right.$��
��3����Ҫ������DB��PΪֱ�������Σ��ɷֱ��������Ƿֱ�Ϊֱ�ǵ������
�١�DB��PΪֱ��ʱ����D��DD1��BC��D1����ͼ5��
��CD��AB����B=60�㣬
���DCD1=60�㣬
DD1=CD•sin��DCD1=3$\sqrt{3}$��CD1=CD•cos��DCD1=3��
��DB��D1=180��-��PB��B-��DB��P=30�㣬
��B��D1=$\frac{D{D}_{1}}{tan��DB��{D}_{1}}$=9��
��BD1=BC+CD1=4+3=7��9��
�������������ڣ�����DB��P����Ϊֱ�ǣ�
�ڡ�DPB��Ϊֱ��ʱ�����ͼ5��
��AD��PB�䣬��DPB��=90�㣬
���ADP=90�㣨��ֱ��ƽ�У��ڴ�����ȣ���
AP=$\frac{AD}{cos��A}$=$\frac{4}{\frac{1}{2}}$=8��
PB=AB-AP=10-8=2t��
��t=1�룮
���ӳ�AD���ӳ�BC��AD���ӳ������A�䣬��B��BM��AA���ڵ�M��BM��PB���ڵ�M�䣬��D��DN��PB�䣬����DM�䣮��ͼ6��
�ߡ�A=��B=60�㣬
���ACA��Ϊ�ȱ������Σ�
�֡�BM��AA���ڵ�M��
��AM=$\frac{1}{2}$AA��=$\frac{1}{2}$AB=5��
�ߡ�PBB��Ҳ�ǵȱ������Σ�
��PM��=B��M�䣬��M��Ϊ�߶�PB����е㣮
��AA���BB�䣬BM��AA�䣬DN��PB�䣬
���ı���DMM��NΪ���Σ�
��NM��=DM=AM-AD=5-4=1��DN=MM��=$\frac{\sqrt{3}}{2}$��AB-PB��=$\frac{\sqrt{3}}{2}$��10-2t��=5$\sqrt{3}$-$\sqrt{3}$t��
�ߡ�PDB��=90�㣬
��DM��=$\frac{1}{2}$PB��=$\frac{1}{2}$PB=t��
�ɹ��ɶ�����֪��DM��2=DN2+NM��2����t2=1+${��5\sqrt{3}-\sqrt{3}t��}^{2}$��
���t=$\frac{15-\sqrt{73}}{2}$�룬��t=$\frac{15+\sqrt{73}}{2}$�룾5�루��ȥ����
�ۺϢ٢ڢۿɵã��������˶������У������Ե�D��P��B��Ϊ�����������Ϊֱ�������Σ�t��ֵΪ1���$\frac{15-\sqrt{73}}{2}$�룮
���� ���⿼���˵ȱ������ε��ж������ʡ��������ε��ж��������Լ����ε��ж������ʣ�����Ĺؼ��ǣ���1���ҳ�������ȫ�ȣ���2������B���E���λ�ã�λ�ò�ͬ���غ�ͼ�β�ͬ�������ͬ����3�������������Ƿֱ�Ϊֱ�ǣ�ͨ���߽ǹ�ϵ�����ɵó����ۣ�


 ѧ���쳵��������������������ϵ�д�
ѧ���쳵��������������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
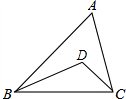 ��ͼ���ڡ�ABC�У���ABC�͡�ACB�Ľ�ƽ���߽��ڵ�D��
��ͼ���ڡ�ABC�У���ABC�͡�ACB�Ľ�ƽ���߽��ڵ�D���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ����ƽ��ֱ������ϵ�У�ֱ��lƽ��x�ᣬ��y���ڵ�A����һ�����ڵĵ�B��l�ϣ�����OB������P��ֱ��OB���˶��������APQ=90�㣬PQ��x���ڵ�C����D��ֱ��OB��ֱ��CA�Ľ��㣬��E��ֱ��CP��y��Ľ��㣬����ACE=��AEC��PD=2OD����PA��PC=��������
��ͼ����ƽ��ֱ������ϵ�У�ֱ��lƽ��x�ᣬ��y���ڵ�A����һ�����ڵĵ�B��l�ϣ�����OB������P��ֱ��OB���˶��������APQ=90�㣬PQ��x���ڵ�C����D��ֱ��OB��ֱ��CA�Ľ��㣬��E��ֱ��CP��y��Ľ��㣬����ACE=��AEC��PD=2OD����PA��PC=��������| A�� | $\frac{{\sqrt{15}}}{5}$ | B�� | $\frac{{\sqrt{15}}}{3}$ | C�� | $\frac{{\sqrt{15}}}{5}$��$\frac{{\sqrt{15}}}{3}$ | D�� | ���϶����� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ڡ�ABC�У���D��BC���е㣬FD��ED���ӳ�ED����P��ʹED=PD������FP��CP�����ж�BE+CF��EF�Ĵ�С��ϵ��
��ͼ���ڡ�ABC�У���D��BC���е㣬FD��ED���ӳ�ED����P��ʹED=PD������FP��CP�����ж�BE+CF��EF�Ĵ�С��ϵ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com