
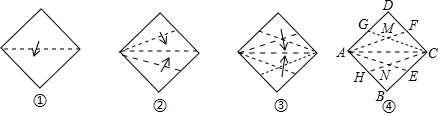
分析 先判定四边形AMCN是菱形,再根据△AOM∽△APF,得出$\frac{AO}{AP}$=$\frac{MO}{FP}$,即$\frac{\sqrt{2}}{2}$=$\frac{MO}{2\sqrt{2}-2}$,求得MN=4-2$\sqrt{2}$,最后根据菱形ANCM的面积=$\frac{1}{2}$AC×MN进行计算即可.
解答 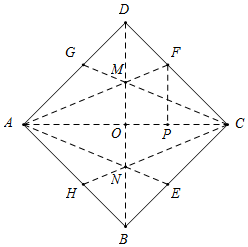 解:如图④,连接BD交AC于O,则BD垂直平分AC,
解:如图④,连接BD交AC于O,则BD垂直平分AC,
由折叠可得,∠MAC=∠MCO=∠NAO=∠NCO=22.5°,
∴AM∥CN,AN∥CM,AM=CM,
∴四边形AMCN是平行四边形,
又∵AM=CM,
∴四边形AMCN是菱形,
∴AN=CN,
∴点M,N在AC的垂直平分线上,即BD经过点M,N,
如图,过F作FP⊥AC于P,则点P与点D关于AF对称,
∴AP=AD=2,
又∵Rt△ACD中,AC=$\sqrt{2}$AD=2$\sqrt{2}$,
∴CP=2$\sqrt{2}$-2,
∴等腰直角三角形CFP中,PF=2$\sqrt{2}$-2,
而等腰直角三角形AOD中,AO=$\frac{AD}{\sqrt{2}}$=$\sqrt{2}$,
∵MO∥FP,
∴△AOM∽△APF,
∴$\frac{AO}{AP}$=$\frac{MO}{FP}$,即$\frac{\sqrt{2}}{2}$=$\frac{MO}{2\sqrt{2}-2}$,
∴2MO=4-2$\sqrt{2}$,即MN=4-2$\sqrt{2}$,
∴菱形ANCM的面积=$\frac{1}{2}$AC×MN=$\frac{1}{2}$×2$\sqrt{2}$×(4-2$\sqrt{2}$)=4$\sqrt{2}$-4,
故答案为:4$\sqrt{2}$-4.
点评 本题属于折叠问题,主要考查了正方形的性质,菱形的判定与性质以及相似三角形的判定与性质的综合应用,解题时注意:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
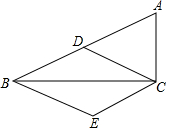 如图,Rt△ABC中点D是AB中点,过点B,点C分别作BE∥CD,CE∥BD.
如图,Rt△ABC中点D是AB中点,过点B,点C分别作BE∥CD,CE∥BD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,直线y=ax+b(a≠0)与双曲线y=$\frac{k}{x}$(k≠0)交于一、三象限内的A,B两点与x轴交于点C,点A的坐标为(2,m),点B的坐标为(n,-2),tan∠BOC=$\frac{2}{5}$.
如图,直线y=ax+b(a≠0)与双曲线y=$\frac{k}{x}$(k≠0)交于一、三象限内的A,B两点与x轴交于点C,点A的坐标为(2,m),点B的坐标为(n,-2),tan∠BOC=$\frac{2}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
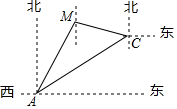 一渔船在海岛A北偏东30°方向的M处遇险,渔船将险情报告给位于A处的救援船后,沿南偏东75°方向向海岛C靠近,同时,从A处出发的救援船沿北偏东60°方向以每小时40$\sqrt{2}$海里的速度匀速航行,30分钟后,救援船在海岛C处恰好追上渔船,那么渔船遇险M处与海岛C的距离是多少海里?($\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7,$\sqrt{6}$≈2.4)
一渔船在海岛A北偏东30°方向的M处遇险,渔船将险情报告给位于A处的救援船后,沿南偏东75°方向向海岛C靠近,同时,从A处出发的救援船沿北偏东60°方向以每小时40$\sqrt{2}$海里的速度匀速航行,30分钟后,救援船在海岛C处恰好追上渔船,那么渔船遇险M处与海岛C的距离是多少海里?($\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7,$\sqrt{6}$≈2.4)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com