
【题目】如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
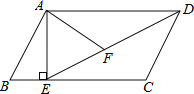
(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=6![]() ,AF=4
,AF=4![]() ,求AE的长.
,求AE的长.
【答案】(1)见解析;(2)6.
【解析】
试题分析:(1)利用对应两角相等,证明两个三角形相似△ADF∽△DEC;
(2)利用△ADF∽△DEC,可以求出线段DE的长度;然后在Rt△ADE中,利用勾股定理求出线段AE的长度.
(1)证明:∵四边形ABCD是平行四边形,∴AB∥CD,AD∥BC,
∴∠C+∠B=180°,∠ADF=∠DEC.
∵∠AFD+∠AFE=180°,∠AFE=∠B,
∴∠AFD=∠C.
在△ADF与△DEC中,
![]()
∴△ADF∽△DEC.
(2)解:∵四边形ABCD是平行四边形,∴CD=AB=8.
由(1)知△ADF∽△DEC,
∴![]() ,∴DE=
,∴DE=![]() =
=![]() =12.
=12.
在Rt△ADE中,由勾股定理得:AE=![]() =
=![]() =6.
=6.


 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF;
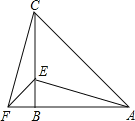
(1)求证:Rt△ABE≌Rt△CBF;
(2)求证:AB=CE+BF;
(3)若∠CAE=30°,求∠ACF度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中正确的是( )
①互为补角的两个角可以都是锐角;②互为补角的两个角可以都是直角;
③互为补角的两个角可以都是钝角;④互为补角的两个角之和是180°.
A. ①② B. ②③ C. ①④ D. ②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=6cm,AC=12cm,动点D以1cm/s 的速度从点A出发到点B止,动点E以2cm/s 的速度从点C出发到点A止,且两点同时运动,当以点A、D、E为顶点的三角形与△ABC相似时,求运动的时间t.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据下列已知条件,能惟一画出△ABC的是( )
A. AB=3,BC=4,CA=8 B. ∠A=60°,∠B=45°,AB=4
C. AB=4,BC=3,∠A=30° D. ∠C=90°,AB=6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子里装有黄色、白色乒乓球共40个,除颜色外其他完全相同.小明从这个袋子中随机摸出一球,放回.通过多次摸球实验后发现,摸到黄色球的概率稳定在15%附近,则袋中黄色球可能有 个.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com