
分析 由于△ADE与△ABC相似,但其对应角不能确定,所以应分两种情况进行讨论.
解答 解:∵S△ADE:S四边形BCED=1:8,
∴S△ADE:S△ABC=1:9,
∴△ADE与△ABC相似比为:1:3,
①若∠AED对应∠B时,
则$\frac{AD}{AC}=\frac{1}{3}$,
∵AC=5cm,
∴AD=$\frac{5}{3}$cm;
②当∠ADE对应∠B时,则$\frac{AD}{AB}=\frac{1}{3}$,
∵AB=6cm,
∴AD=2cm;
故答案为:$2或\frac{5}{3}$.
点评 本题考查的是相似三角形的性质,相似三角形的对应边成比例,相似三角形的面积比等于相似比的平方,意识到有两种情况分类讨论是解决问题的关键.


 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案科目:初中数学 来源: 题型:解答题
类型 编号 | 一 | 二 | 三 | 四 | 五 | 六 | 七 | 八 | 九 | 十 |
| 甲种电子钟 | 1 | -3 | -4 | 4 | 2 | -2 | 2 | -1 | -1 | 2 |
| 乙种电子钟 | 4 | -3 | -1 | 2 | -2 | 1 | -2 | 2 | -2 | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
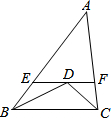 如图,在△ABC中,∠ABC和∠ACB的平分线交于点D,过点D作EF∥BC交AB于E 交AC于F,若AB=10,BC=7,AC=8,则△AEF的周长为( )
如图,在△ABC中,∠ABC和∠ACB的平分线交于点D,过点D作EF∥BC交AB于E 交AC于F,若AB=10,BC=7,AC=8,则△AEF的周长为( )| A. | 15 | B. | 16 | C. | 17 | D. | 18 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
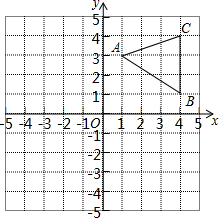 如图,已知△ABC三个顶点坐标分别是A(1,3),B(4,1),C(4,4).
如图,已知△ABC三个顶点坐标分别是A(1,3),B(4,1),C(4,4).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
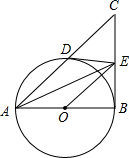 如图,△ABC中∠ABC=90°,以AB为直径作⊙O,与AC交于点D,点E为DC中点,连DE
如图,△ABC中∠ABC=90°,以AB为直径作⊙O,与AC交于点D,点E为DC中点,连DE查看答案和解析>>
科目:初中数学 来源: 题型:解答题
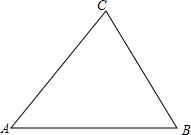 已知:△ABC.
已知:△ABC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com