
【题目】如图,A(m,0),B(0,n),以B点为直角顶点在第二象限作等腰直角△ABC.
(1)求C点的坐标.
(2)在y轴右侧的平面内是否存在一点P,使△PAB与△ABC全等?若存在,求出P点坐标,若不存在,请说明理由.
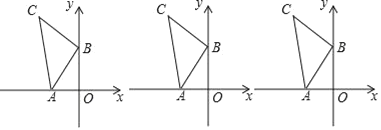
【答案】(1)点C的坐标为(﹣n,n﹣m);(2)存在,P点坐标为(n,n+m)或(m+n,m).
【解析】
(1)过点C作CD⊥y轴于点D,由△ABC为等腰直角三角形即可得出∠ABC=90°、AB=BC,通过角的计算即可得出∠ABO=∠BCD,再结合∠CDB=∠BOA=90°即可利用AAS证出△ABO和△BCD,由此即可得出BD、CD的长度,进而可得出点C的坐标;
(2)△PAB与△ABC全等分两种情况:①当∠ABP=90°时,根据∠ABC=∠ABP=90°、△ABC≌△ABP,即可得出点C、P关于点B对称,结合点B、C的坐标即可得出点P的坐标;②当∠BAP=90°时,由∠ABC=∠BAP=90°即可得出BC∥AP,根据△ABC≌△BAP即可得出BC=AP,进而可找出四边形APBC为平行四边形,结合点A、B、C的坐标即可找出点P的坐标.综上即可得出结论.
解:(1)过点C作CD⊥y轴于点D,如图1所示.

∵△ABC为等腰直角三角形,
∴∠ABC=90°,AB=BC.
∵CD⊥BD,BO⊥AO,
∴∠CDB=∠BOA=90°.
∵∠CBD+∠ABO=90°,∠CBD+∠BCD=90°,
∴∠ABO=∠BCD.
∴△ABO≌△BCD(AAS),
∴BD=AO,CD=BO,
∵A(m,0),B(0,n),
∴BD=﹣m,CD=n,
∴点C的坐标为(﹣n,n﹣m).
(2)△PAB与△ABC全等分两种情况:
①当∠ABP=90°时,如图2所示.

∵∠ABC=∠ABP=90°,△ABC≌△ABP,
∴点C、P关于点B对称,
∵C(﹣n,n﹣m),B(0,n),
∴点P的坐标为(n,n+m);
②当∠BAP=90°时,如图3所示.

∵△ABC≌△BAP,
∴∠ABC=∠BAP=90°,BC=AP,
∴BC∥AP,
∴四边形APBC为平行四边形.
∵A(m,0)、B(0,n),C(﹣n,n﹣m),
∴点P的坐标为(m+n,m).
综上所述:在y轴右侧的平面内存在一点P,使△PAB与△ABC全等,P点坐标为(n,n+m)或(m+n,m).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,已知∠1=∠2,AC=AD,要使△ABC≌△AED,还需添加一个条件,那么在①AB=AE,②BC=ED,③∠C=∠D,④∠B=∠E,这四个关系中可以选择的是( )
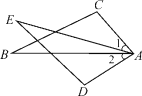
A. ①②③ B. ①②④ C. ①③④ D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,直线AB交CD于点O,OE平分∠BOD,OF平分∠COB,∠AOD:∠BOE=5:2,则∠AOF等于( )

A. 140° B. 130° C. 120° D. 110°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,AB=AC,D是AC边上一动点,CE⊥BD于E.

(1)如图(1),若BD平分∠ABC时,①求∠ECD的度数;②延长CE交BA的延长线于点F,补全图形,探究BD与EC的数量关系,并证明你的结论;
(2)如图(2),过点A作AF⊥BE于点F,猜想线段BE,CE,AF之间的数量关系,并证明你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在Rt△ABC中,∠C=90°,AD是△ABC的角平分线,DE⊥AB,垂足为点E,AE=BE.
(1)猜想:∠B的度数,并证明你的猜想.
(2)如果AC=3cm,CD=2cm,求△ABD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019 年 3 月 31 日,南京地铁新的价格方案正式实施,实行消费累进优惠.普通成人每月持卡乘坐地铁,当消费累计金额不超过 150 元时,每次乘坐地铁的票价打 9.5 折;当消费累计金 额超过 150 元时,达到规定的消费累计金额后的乘次,票价所打折扣如下表所示:
消费累计金额 | 折扣 |
| 9折 |
| 8折 |
| 9.5折 |
小明上、下班每次乘坐的地铁单程票价为 10元,2019年 4月份他上、下班持卡共乘坐了 40次.
(1)填表:
第1 次 | 第2 次 | … | 第15次 | 第16次 | 第17次 | … | |
消费累计 金额(元) | 9.5 | 19 | … | 142.5 | 152 | … |
span>
(2)小明当月第几次乘车后,消费累计金额超过 20元?(用一元一次不等式解决问题)
(3)小明 4月份上、下班持卡乘坐地铁的消费累计金额为 元.
查看答案和解析>>
科目:初中数学 来源: 题型:
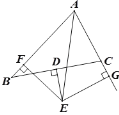
【题目】如图,在△ABC中,D为BC的中点,DE⊥BC交∠BAC 的平分线AE于E,EF⊥AB于F,EG⊥AC交AC延长线于G. AB=6, AC=3,求BF 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把抛物线y=ax![]() +bx+c的图象先向右平移3个单位,再向下平移2个单位,所得的图象的解析式是y=x
+bx+c的图象先向右平移3个单位,再向下平移2个单位,所得的图象的解析式是y=x![]() -3x+5,则a+b+c=__________。
-3x+5,则a+b+c=__________。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上, 老师要求同学们利用三角板画两条平行线.老师说苗苗和小华两位同学画法都是正确的,两位同学的画法如下:
苗苗的画法:

①将含30°角的三角尺的最长边与直线a重合,另一块三角尺最长边与含30°角的三角尺的最短边紧贴;
②将含30°角的三角尺沿贴合边平移一段距离,画出最长边所在直线b,则b//a.
小华的画法:

①将含30°角三角尺的最长边与直线a重合,用虚线做出一条最短边所在直线;
②再次将含30°角三角尺的最短边与虚线重合,画出最长边所在直线b,则b//a.
请在苗苗和小华两位同学画平行线的方法中选出你喜欢的一种,并写出这种画图的依据.
答:我喜欢__________同学的画法,画图的依据是__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com