
����Ŀ��2016��������������ڳе��оٰ죬���е���ʨ��������Ϊ�·���յ�Ϊ�������ģ���������Ϊֱ�ߣ�������������A��B��������㣬���мף�������������Ա���ֱ��A��B���������ͬʱ��������ֱ�����������յ�C���������ģ�����ͼ1��ʾ����ס������˳���xh����B��ľ���ֱ�Ϊy��km��y��km��y����y����x�ĺ�����ϵ��ͼ2��ʾ��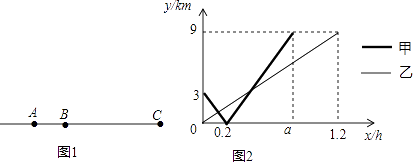
��1���ӷ����A���յ�C�ľ���Ϊkm��a=h��
��2�����������ʱx��ֵ��
��3����������֮��ľ���Ӧ������1kmʱ����Ϊ��ѷ�����룬�Ӽס��������������յ���ǰ��������ѷ�������ʱ���ж��
���𰸡�
��1��12,0.8
��2���⣺���Ҷ�Ӧ�ĺ�������ʽΪ��y=kx��
1.2k=9����k=7.5��
���Ҷ�Ӧ�ĺ�������ʽΪ��y=7.5x��
��x��0.2ʱ�����Ӧ�ĺ�������ʽΪy=mx+n��
![]() ����
���� ![]() ��
��
����x��0.2ʱ����Ӧ�ĺ�������ʽΪy=15x��3��
��7.5x=15x��3����x=0.4��
����������ʱx��ֵ��0.4
��3���⣺������ɵã�
15x��3��7.5x��1����x�� ![]() ��
��
�� ![]() ��
��
��ס��������������յ���ǰ��������ѷ�������ʱ���� ![]() h
h
���������⣺��1����ͼ��ɵã�
�ӷ����A���յ�C�ľ���Ϊ��3+9=12��km����
a=0.2+9�£�3��0.2��=0.8��
���Դ��ǣ�12��0.8��
�����㾫����������Ĺؼ���������ȷ��һ�κ����ı���ʽ�����֪ʶ������ȷ��һ��һ�κ�������Ҫȷ��һ�κ�������ʽy=kx+b��k������0���еij���k��b�������������һ�㷽���Ǵ���ϵ������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
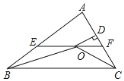
����Ŀ����ͼ����![]() �У�
��![]() ��
��![]() ��ƽ�����ཻ�ڵ�O����O����
��ƽ�����ཻ�ڵ�O����O����![]() ��AB�ڵ�E����AC�ڵ�F������O��
��AB�ڵ�E����AC�ڵ�F������O��![]() ��D�������ĸ����ۣ�
��D�������ĸ����ۣ�
![]()
![]()
![]() ��O��
��O��![]() ���ߵľ������
���ߵľ������![]() ��
��![]() ��
��![]() ����
����![]() ����ȷ�Ľ�����
����ȷ�Ľ�����![]() ����
����![]() ����
����
A. 1��B. 2��C. 3��D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ���ڴ�����4����ȫ��ͬ��С�����Ƿֱ���Ϊ1��2��3��4�����������һ��С�Żأ������������һ��С��������������С��ı�ŵĺ�Ϊ�����ĸ����ǣ� ��
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AD�ǡ�ABC�Ľ�ƽ���ߣ�DE��DF�ֱ��ǡ�ABD�͡�ACD�ĸߣ������н��ۣ�
��OA=OD��
��AD��EF��
��AE+DF=AF+DE��
�ܵ���BAC=90��ʱ���ı���AEDF�������Σ�
����һ����ȷ���ǣ� ��
A.�٢ڢ�
B.�ڢۢ�
C.�٢ۢ�
D.�٢ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ijͬѧ��ɳ̲����ʯ�ڰڳɵ�С���ӣ�

�۲�ͼ�εı仯���ɣ�д����n��С��������___________________��ʯ�ӣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ABCD�У�BC=3��AB=8��E��FΪAB��CD���ϵ��е㣬��ͼ1��A��ԭ�㴦����B��y���������ϣ���C�ڵ�һ���ޣ�����A��ԭ���������x��������ÿ��1����λ���ȵ��ٶ��˶������B��֮��y���»�������������ABCD��ƽ���ϻ�������ͼ2�����˶�ʱ���ʾΪt�룬��B����ԭ��ʱֹͣ�˶���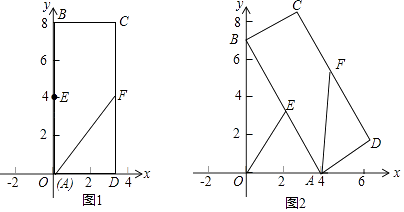
��1����t=0ʱ�����F�����꼰FA�ij��ȣ�
��2����t=4ʱ����OE�ij�����BAO�Ĵ�С��
��3�����t=0��t=4��һʱ�ε�E�˶�·�ߵij���
��4�����Ե�FΪԲ�ģ�FAΪ�뾶��Բ������������ʱ����t��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ���
����֪����![]() ����Ҫ�ⲻ��ʽ
����Ҫ�ⲻ��ʽ![]() �����ǿ��Է��������ȥ������ֵ���ţ�ת��Ϊ������Ϥ�IJ���ʽ��������˼·�����������½ⷨ��
�����ǿ��Է��������ȥ������ֵ���ţ�ת��Ϊ������Ϥ�IJ���ʽ��������˼·�����������½ⷨ��
��:��1����![]() ����
����![]() ʱ��
ʱ��![]()
���������ʽ���ã�![]()
������![]() ����
����![]()
��2����![]() ����
����![]() ʱ��
ʱ��![]()
���������ʽ���ã�![]()
������![]() ����
����![]()
�� ��ͼ��![]()
�ۺϣ�1������2��ԭ����ʽ�Ľ�Ϊ��![]()
��������˼�룬��̽���������![]() ��С�⣺
��С�⣺
![]() ��
��
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ͼa��һ����Ϊ![]() ����Ϊ
����Ϊ![]() �ij����Σ�����
�ij���������![]() >
>![]() ��, ��ͼ�������ü������ֳ��Ŀ�С������, Ȼ��ͼ
��, ��ͼ�������ü������ֳ��Ŀ�С������, Ȼ��ͼ![]() ����״ƴ��һ�������Σ�
����״ƴ��һ�������Σ�
(1)�����������ֲ�ͬ�ķ�����ʾͼ![]() �е���Ӱ���ֵ���� �� ��
�е���Ӱ���ֵ���� �� ��
����д������ʽ��![]() ��
��![]() ��
��![]() ֮��Ĺ�ϵ�� ��
֮��Ĺ�ϵ�� ��
��2����![]() ����
����![]() ��ֵ��
��ֵ��
��3����֪![]() ����
����![]() ��ֵ��
��ֵ��


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ����ֱ��y=kx+b������A����30��0���͵�B��0��15����ֱ��y=x+5��ֱ��y=kx+b�ཻ�ڵ�P����y�ύ�ڵ�C��

��1����ֱ��y=kx+b�Ľ���ʽ��
��2�����PBC�������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com