
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于二、四象限内的A、B两点,与x轴交于C点,点A的坐标为(- 3,4),点B的坐标为(6,n).
的图象交于二、四象限内的A、B两点,与x轴交于C点,点A的坐标为(- 3,4),点B的坐标为(6,n).
(1)求该反比例函数和一次函数的解析式;
(2)连接OB,求△AOB 的面积;
(3)在x轴上是否存在点P,使△APC是直角三角形. 若存在,求出点P的坐标;若不存在,请说明理由.

【答案】(1)反比例函数的解析式为y=﹣![]() ; 一次函数的解析式为y=﹣
; 一次函数的解析式为y=﹣![]() x+2; (2)
x+2; (2)![]() ;(3)存在,满足条件的P点坐标为(﹣3,0)、(﹣
;(3)存在,满足条件的P点坐标为(﹣3,0)、(﹣![]() ,0).
,0).
【解析】试题分析:(1)先把![]() 代入
代入![]() 得到
得到![]() 的值,从而确定反比例函数的解析式为
的值,从而确定反比例函数的解析式为![]() ;再利用反比例函数解析式确定B点坐标为
;再利用反比例函数解析式确定B点坐标为![]() ,然后运用待定系数法确定所求的一次函数的解析式为
,然后运用待定系数法确定所求的一次函数的解析式为![]()
![]()
![]() 即可求得.
即可求得.
(3)过A点作![]() 轴于
轴于![]() ,
, ![]() 交x轴于
交x轴于![]() ,则
,则![]() 点的坐标为
点的坐标为![]() ;再证明
;再证明![]() 利用相似比计算出
利用相似比计算出![]() 则
则![]() ,所以
,所以![]() 点的坐标为
点的坐标为![]() ,于是得到满足条件的P点坐标.
,于是得到满足条件的P点坐标.
试题解析:
![]() 将
将![]() 代入
代入![]() ,得
,得![]()
∴反比例函数的解析式为![]() ;
;
将![]() 代入
代入![]() ,得
,得![]()
解得![]()
![]()
将![]() 和
和![]() 分别代入
分别代入![]() 得
得![]() ,
,
解得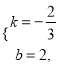 ,
,
∴所求的一次函数的解析式为![]()
(2)当![]() 时,
时, ![]() 解得:
解得: ![]()
![]()
![]()
![]()
(3)存在.
过A点作![]() 轴于
轴于![]() ,
, ![]() 交x轴于
交x轴于![]() ,如图,
,如图,
![]()
![]() 点坐标为
点坐标为![]()
![]() 点的坐标为
点的坐标为![]()
![]()
![]()
而![]()
![]()
![]()
![]() 即
即![]()
![]()
![]()
![]() 点的坐标为
点的坐标为![]()
∴满足条件的![]() 点坐标为
点坐标为![]()
![]()


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标系![]() 中的点P和图形G,给出如下的定义:若在图形G上存在一点Q ,使得P、Q之间的距离等于1,则称P为图形G的关联点.
中的点P和图形G,给出如下的定义:若在图形G上存在一点Q ,使得P、Q之间的距离等于1,则称P为图形G的关联点.
(1)当⊙O的半径为1时:
①点![]() ,
, ![]() ,
, ![]() 中,⊙O的关联点有_____________________.
中,⊙O的关联点有_____________________.
②直线经过(0,1)点,且与![]() 轴垂直,点P在直线上.若P是⊙O的关联点,求点P的横坐标
轴垂直,点P在直线上.若P是⊙O的关联点,求点P的横坐标![]() 的取值范围.
的取值范围.
(2)已知正方形ABCD的边长为4,中心为原点,正方形各边都与坐标轴垂直.若正方形各边上的点都是某个圆的关联点,求圆的半径![]() 的取值范围.
的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,D是边AC上一点,连接BD,将△BCD绕点B逆时针旋转60°,得到△BAE,连接ED,下列结论正确的有( )个.
①△BED是等边三角形;②AE∥BC; ③△ADE的周长等于BD+BC;④∠ADE=∠DBC.
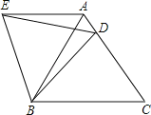
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
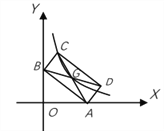
【题目】如图,矩形ABCD的两个顶点A、B分别落在x、y轴上,顶点C、D位于第一象限,且OA=3,OB=2,对角线AC、BD交于点G,若曲线y![]() 经过点C、G,则k=__________.
经过点C、G,则k=__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】边长为4的等边![]() 与等边
与等边![]() 互相重合,将
互相重合,将![]() 沿直线L向左平移m个单位长度,将
沿直线L向左平移m个单位长度,将![]() 向右也平移m个单位长度,若
向右也平移m个单位长度,若![]() ,则m=________;若C、E是线段BF的三等分点时,m=________.
,则m=________;若C、E是线段BF的三等分点时,m=________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx-3交x轴于点A(﹣3,0),点B(1,0),交y轴于点E.点C是点A关于点B的对称点,点F是线段BC的中点,直线![]() 过点F且与y轴平行.直线y=kx+3过点C,交y轴于D点.
过点F且与y轴平行.直线y=kx+3过点C,交y轴于D点.
(1)求抛物线的函数表达式;
(2)点K为线段AB上一动点,过点K作x轴的垂线与直线CD交于点H,与抛物线交于点G,求线段HG长度的最大值;
(3)在直线![]() 上取点M,在抛物线上取点N,使以点A,C,M,N为顶点的四边形是平行四边形,求点N的坐标.
上取点M,在抛物线上取点N,使以点A,C,M,N为顶点的四边形是平行四边形,求点N的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列一组图形中点的个数,其中第1个图中共有4个点,第2个图中共有10个点,第3个图中共有19个点,…,按此规律第6个图中共有点的个数是( )
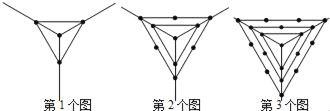
A.46B.63C.64D.73
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某楼盘一楼是车库(暂不出售),二楼至二十三楼均为商品房(对外销售).商品房售价方案如下:第八层售价为4000元![]() 米
米![]() ,从第八层起每上升一层.每平方米的售价增加50元;反之,楼层每下降一层,每平方米的售价减少30元.已知商品房每套面积均为120平方米,开发商为购买者制定了两种购房方案:方案一:购买者先交纳首付金额(商品房总价的
,从第八层起每上升一层.每平方米的售价增加50元;反之,楼层每下降一层,每平方米的售价减少30元.已知商品房每套面积均为120平方米,开发商为购买者制定了两种购房方案:方案一:购买者先交纳首付金额(商品房总价的![]() ,再办理分期付款(即贷款).方案二:购买者若一次付清所有房款,则享受
,再办理分期付款(即贷款).方案二:购买者若一次付清所有房款,则享受![]() 的优惠,并免收五年物业管理费(已知每月物业管理费为
的优惠,并免收五年物业管理费(已知每月物业管理费为![]() 元).
元).
(1)请用含楼层(![]() ,
,![]() 是正整数)的代数式表示售价y(元/平方米);
是正整数)的代数式表示售价y(元/平方米);
(2)小张已筹到160000元,若用方案一购房,他可以首付哪些楼层的商品房呢?
(3)老王想在此楼盘买房,有人建议老王使用方案二购买第十六层,但他认为此方案还不如不免收物业管理费而直接再多享受![]() 的优惠划算.你认为老王的说法一定正确吗?请用具体数据阐明你的看法.
的优惠划算.你认为老王的说法一定正确吗?请用具体数据阐明你的看法.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形ABCD的两条对角线相交于点O,过点 A作AG⊥BD分别交BD、BC于点G、E.
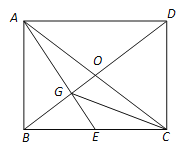
(1)求证:BE2=EGEA;
(2)连接CG,若BE=CE,求证:∠ECG=∠EAC.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com