
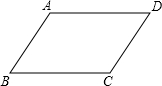
 如图,请在下列四个关系中,选出两个恰当的关系作为条件,推出四边形ABCD是平行四边形,并予以证明.(写出一种即可)
如图,请在下列四个关系中,选出两个恰当的关系作为条件,推出四边形ABCD是平行四边形,并予以证明.(写出一种即可)

 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:初中数学 来源: 题型:
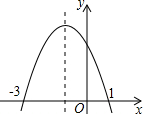 二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象答下列问题:
二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:
 已知有理数a、b、c在数轴上的位置如图所示,且|a|=|b|.
已知有理数a、b、c在数轴上的位置如图所示,且|a|=|b|.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com