
| 月份n(月) | 1 | 2 |
| 成本y(万元/件) | 11 | 12 |
| 需求量x(件/月) | 120 | 100 |
分析 (1)设y=a+$\frac{b}{x}$,将表中相关数据代入可求得a、b,根据12=18-(6+$\frac{600}{x}$),则$\frac{600}{x}$=0可作出判断;
(2)将n=1、x=120代入x=2n2-2kn+9(k+3)可求得k的值,先由18=6+$\frac{600}{x}$求得x=50,根据50=2n2-26n+144可判断;
(3)第m个月的利润W=x(18-y)=18x-x(6+$\frac{600}{x}$)=24(m2-13m+47),第(m+1)个月的利润为W′=24[(m+1)2-13(m+1)+47]=24(m2-11m+35),分情况作差结合m的范围,由一次函数性质可得.
解答 解:(1)由题意,设y=a+$\frac{b}{x}$,
由表中数据可得:$\left\{\begin{array}{l}{11=a+\frac{b}{120}}\\{12=a+\frac{b}{100}}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=6}\\{b=600}\end{array}\right.$,
∴y=6+$\frac{600}{x}$,
由题意,若12=18-(6+$\frac{600}{x}$),则$\frac{600}{x}$=0,
∵x>0,
∴$\frac{600}{x}$>0,
∴不可能;
(2)将n=1、x=120代入x=2n2-2kn+9(k+3),得:120=2-2k+9k+27,
解得:k=13,
∴x=2n2-26n+144,
将n=2、x=100代入x=2n2-26n+144也符合,
∴k=13;
由题意,得:18=6+$\frac{600}{x}$,
解得:x=50,
∴50=2n2-26n+144,即n2-13n+47=0,
∵△=(-13)2-4×1×47<0,
∴方程无实数根,
∴不存在;
(3)第m个月的利润为W,
W=x(18-y)=18x-x(6+$\frac{600}{x}$)
=12(x-50)
=24(m2-13m+47),
∴第(m+1)个月的利润为W′=24[(m+1)2-13(m+1)+47]=24(m2-11m+35),
若W≥W′,W-W′=48(6-m),m取最小1,W-W′取得最大值240;
若W<W′,W′-W=48(m-6),由m+1≤12知m取最大11,W′-W取得最大值240;
∴m=1或11.
点评 本题主要考查二次函数的应用,理解题意准确梳理所涉变量,并熟练掌握待定系数法求函数解析式、利润的相等关系列出解析式是解题的关键.


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 宏兴企业接到一批产品的生产任务,按要求必须在14天内完成.已知每件产品的出厂价为60元.工人甲第x天生产的产品数量为y件,y与x满足如下关系:y=$\left\{\begin{array}{l}7.5x({0≤x≤4})\\ 5x+10({4<x≤14})\end{array}$.
宏兴企业接到一批产品的生产任务,按要求必须在14天内完成.已知每件产品的出厂价为60元.工人甲第x天生产的产品数量为y件,y与x满足如下关系:y=$\left\{\begin{array}{l}7.5x({0≤x≤4})\\ 5x+10({4<x≤14})\end{array}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
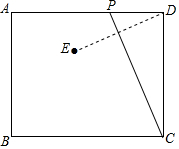 如图,已知矩形ABCD中,AB=4,AD=m,动点P从点D出发,在边DA上以每秒1个单位的速度向点A运动,连接CP,作点D关于直线PC的对称点E,设点P的运动时间为t(s).
如图,已知矩形ABCD中,AB=4,AD=m,动点P从点D出发,在边DA上以每秒1个单位的速度向点A运动,连接CP,作点D关于直线PC的对称点E,设点P的运动时间为t(s).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
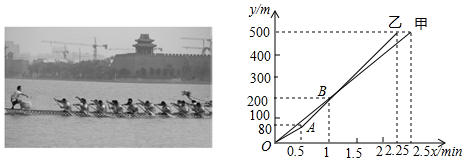
| A. | 乙队比甲队提前0.25min到达终点 | |
| B. | 当乙队划行110m时,此时落后甲队15m | |
| C. | 0.5min后,乙队比甲队每分钟快40m | |
| D. | 自1.5min开始,甲队若要与乙队同时到达终点,甲队的速度需要提高到255m/min |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
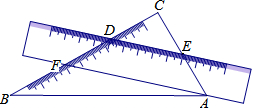 一把直尺和一块三角板ABC(含30°、60°角)摆放位置如图所示,直尺一边与三角板的两直角边分别交于点D、点E,另一边与三角板的两直角边分别交于点F、点A,且∠CDE=40°,那么∠BAF的大小为( )
一把直尺和一块三角板ABC(含30°、60°角)摆放位置如图所示,直尺一边与三角板的两直角边分别交于点D、点E,另一边与三角板的两直角边分别交于点F、点A,且∠CDE=40°,那么∠BAF的大小为( )| A. | 40° | B. | 45° | C. | 50° | D. | 10° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
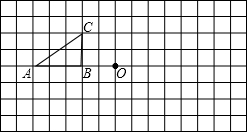
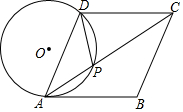 如图,在菱形ABCD中,点P在对角线AC上,且PA=PD,⊙O是△PAD的外接圆.
如图,在菱形ABCD中,点P在对角线AC上,且PA=PD,⊙O是△PAD的外接圆.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com