
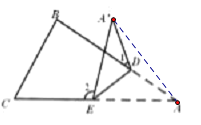
����Ŀ������1������һ�š�ABCֽƬ����D��E�ֱ��ǡ�ABC�������㣬����ֱ��DE�۵���
��1��̽��1������۳�ͼ�ٵ���״��ʹA������CE�ϣ����1���A��������ϵ�� ��
��2��̽��2������۳�ͼ�ڵ���״�������1+��2�͡�A��������ϵ�� ��
��3��̽��3������۳�ͼ�۵���״�������1����2�͡�A��������ϵ����˵�����ɣ�

��4������2��������1�ƹ㣬��ͼ�ܣ����ı���ABCDֽƬ��EF�۵���ʹ��A��B�����ı���EFCD���ڲ�ʱ����1+��2���A����B֮���������ϵ�� .
���𰸡���1��![]() ;��2��
;��2��![]() ;��3��������;��4��
;��3��������;��4��![]()
��������
��1������������������ʿɵã�
��2�����ı���![]() �У��ڽǺ�Ϊ360������BDA=��CEA=180�����������������������нǶ�ת���ɵù�ϵʽ��
�У��ڽǺ�Ϊ360������BDA=��CEA=180�����������������������нǶ�ת���ɵù�ϵʽ��
��3������ͼ�����ݣ�1���ɵ���1=2��![]() ����2=2��
����2=2��![]() ���Ӷ��Ƶ�����ϵʽ��
���Ӷ��Ƶ�����ϵʽ��
��4������ƽ�ǵĶ����Լ��ı��ε��ڽǺͶ������루2������˼·̽�֣��ɵù�ϵʽ��
��1���ߡ�![]() �ǡ�EDA�۵��õ�
�ǡ�EDA�۵��õ�
���A=��![]()
�ߡ�1�ǡ�![]() �����
�����
���1=��A+��![]()
��![]() ��
��
��2�������ı���![]() �У��ڽǺ�Ϊ360��
�У��ڽǺ�Ϊ360��
���A+![]() +��
+��![]() ��
��![]() =360��
=360��
ͬ������A=��![]()
��2��A+��![]() ��
��![]() =360��
=360��
�ߡ�BDA=��CEA=180
���1+��![]() ��
��![]() +��2=360��
+��2=360��
��![]() ��
��
��3��������ϵ��![]()
���ɣ�����ͼ������![]()
�ɣ�1����֪����1=2��![]() ����2=2��
����2=2��![]()
��![]() ��
��
��4�����۵�����֪����2=180����2��AEF����1=180����2��BFE
��ӵã�![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ţ�2������֯��һ���ʶ��������ס������Ӹ�10�˵ı����ɼ���10���ƣ����±�����λ���֣���
�� | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
�� | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
��1���ӳɼ�����λ�����֣��Ҷӳɼ����������֣�
��2�������Ҷӳɼ���ƽ�����ͷ��
��3����֪�ӳɼ��ķ�����1.4��2 �� ��ɼ���Ϊ��������ӣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���C=90�㣬BDƽ�֡�ABC����AC���ڵ�D����O��AB��һ�㣬��O��B��D���㣬�ҷֱ�AB��BC�ڵ�E��F��
��1����֤��AC�ǡ�O�����ߣ�
��2����֪AB=10��BC=6�����O�İ뾶r ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����壺��ѧ����ϣ�����ʦ�������¶��壺��һ��Ա���ȶ���һ��Ա߲���ȵ��ı��ν����Ե��ı��Σ�
���⣺
��1����ͼ1����֪A��B��C�ڸ�㣨С�����εĶ��㣩�ϣ����ڷ���ͼ�л����Ը��Ϊ���㣬AB��BCΪ�ߵ������Ե��ı���ABCD��
��2����ͼ2����Բ�ڽ��ı���ABCD�У�AB�ǡ�O��ֱ����AC=BD����֤���ı���ABCD�ǶԵ��ı��Σ�
��3����ͼ3����Rt��PBC�У���PCB=90�㣬BC=11��tan��PBC= ![]() ����A��BP���ϣ���AB=13����Բ����PC���ҵ����������ĵ�D��ʹ�ı���ABCDΪ�Ե��ı��Σ������CD�ij���
����A��BP���ϣ���AB=13����Բ����PC���ҵ����������ĵ�D��ʹ�ı���ABCDΪ�Ե��ı��Σ������CD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У� ![]() ����D��BC���ڵ�ֱ���ϣ���E������AC�ϣ���
����D��BC���ڵ�ֱ���ϣ���E������AC�ϣ���![]() ������DE��
������DE��
��1����ͼ�٣���![]() ��
�� ![]() ����
����![]() �Ķ�����
�Ķ�����
��2����ͼ�ڣ���![]() ��
�� ![]() ����
����![]() �Ķ�����
�Ķ�����
��3������D��ֱ��BC�ϣ������B��C�غϣ��˶�ʱ����̽��![]() ��
��![]() ��������ϵ����˵�����ɣ�
��������ϵ����˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1�����ı���ABCD�У�AB��AD����BAD��120������B����ADC��90����E��F�ֱ���BC��CD�ϵĵ㣮�ҡ�EAF��60����̽��ͼ���߶�BE��EF��FD֮���������ϵ��
С��ͬѧ̽��������ķ����ǣ��ӳ�FD����G��ʹDG��BE������AG����֤����ABE�ա�ADG����֤����AEF�ա�AGF���ɵó����ۣ����Ľ���Ӧ���� ����

̽�����죺
��ͼ2�������ı���ABCD�У�AB��AD����B����D��180����E��F�ֱ���BC��CD�ϵĵ㣬�ҡ�EAF��![]() ��BAD�����������Ƿ���Ȼ��������˵�����ɣ�
��BAD�����������Ƿ���Ȼ��������˵�����ɣ�
ʵ��Ӧ�ã�
��ͼ3����ij�ξ�����ϰ�У���ͧ����ָ�����ģ�O������ƫ��30����A������ͧ����ָ��������ƫ��70����B������������ͧ��ָ�����ĵľ�����ȣ��ӵ��ж�ָ���ͧ��������������60����/Сʱ���ٶ�ǰ������ͧ���ر�ƫ��50���ķ�����80����/Сʱ���ٶ�ǰ��1.5Сʱ��ָ�����Ĺ۲�ס�������ͧ�ֱ�E��F����������֮ͧ��ļн�Ϊ70���������ʱ����֮ͧ��ľ��룿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ж���ʽ�ij˷��У�������ƽ���ʽ������У� ��
A.��x+![]() ������x��
������x��![]() ��B.����2+m������m��2��
��B.����2+m������m��2��
C.����a+b����a��b��D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��̽�����֣���ͼ��һ�����쵯����ʵ��ͼ������ͷ��ϵ��Ƥ�����Ƥ����γ�ƽ��ʾ��ͼ��ͼ1ͼ2�����������߿ɿ�����ƽ�еģ���AB��CD�����С��̽����APC ���A����C֮���������ϵ����֪AB��CD����P����ֱ��AB��ֱ��CD�ϣ���ͼ1�У��ǻ�С�鷢�֣���APC����A+��C��

�ǻ�С��������˼���ģ����� P �� PQ��AB������
��1�����㰴���ǻ�С�����ĸ��������֤�����̣�
��2������ͼ2�У��²��APC���A����C ֮���������ϵ�������֤����
����ͼ3����֪AB��CD���������������֮���������ϵΪ ����ֱ����գ�
��3����˼С���������ͼ4��ͼ5��AB��CD��AF��CF�ֱ�ƽ�֡�BAP����DCP
����ͼ4�У��²��AFC���APC֮���������ϵ����֤����
����ͼ5�У���AFC���APC֮���������ϵΪ ����ֱ����գ�

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com