Question

8．如图，以菱形ABCD对角线交点为坐标原点，建立平面直角坐标系，A、B两点的坐标分别为（-2$\sqrt{5}$，0）、（0，-$\sqrt{5}$），直线DE⊥DC交AC于E，动点P从点A出发，以每秒2个单位的速度沿着A→D→C的路线向终点C匀速运动，设△PDE的面积为S（S≠0），点P的运动时间为t秒．
（1）求直线DE的解析式；
（2）求S与t之间的函数关系式，并写出自变量t的取值范围；
（3）当t为何值时，∠EPD+∠DCB=90°？并求出此时直线BP与直线AC所夹锐角的正切值．

Answer 1

分析 （1）先有菱形的对称性得出点C，D坐标，然后用∠DCO的正切值，以及等角的三角函数值相等列出方程，最后用待定系数法求出直线DE解析式．
（2）先求出菱形的边长，再求出EF，分点P在AD和DC边上，用面积公式求解；
（3）先求出∠EPD=∠ADE，分两种情况用由菱形的边长建立方程求出时间t，用相似三角形的比例式建立方程求出OQ，解直角三角形即可．

解答 解：由菱形的对称性可得，C（2$\sqrt{5}$，0），D（0，$\sqrt{5}$），
∴OD=$\sqrt{5}$，OC=2$\sqrt{5}$，tan∠DCO=$\frac{OD}{OC}$=$\frac{1}{2}$，
∵DE⊥DC，
∴∠EDO+∠CDO=90°，
∵∠DCO+∠CD∠=90°，
∴∠EDO=∠DCO，
∵tan∠EDO=tan∠DCO=$\frac{1}{2}$，
∴$\frac{OE}{OD}=\frac{OE}{\sqrt{5}}=\frac{1}{2}$，
∴OE=$\frac{\sqrt{5}}{2}$，
∴E（-$\frac{\sqrt{5}}{2}$，0），
∴D（0，$\sqrt{5}$），
∴直线DE解析式为y=2x+$\sqrt{5}$，
（2）由（1）得E（-$\frac{\sqrt{5}}{2}$，0），
∴AE=AO-OE=2$\sqrt{5}$-$\frac{\sqrt{5}}{2}$=$\frac{3\sqrt{5}}{2}$，
根据勾股定理得，DE=$\sqrt{O{D}^{2}+O{E}^{2}}$=$\frac{5}{2}$，
∴菱形的边长为5，
如图1，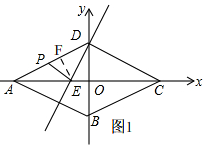

过点E作EF⊥AD，
∴sin∠DAO=$\frac{EF}{AE}=\frac{OD}{AD}$，
∴EF=$\frac{OD×AE}{AD}$=$\frac{3}{2}$，
当点P在AD边上运动，即0≤t＜$\frac{5}{2}$，
S=$\frac{1}{2}$PD×EF=$\frac{1}{2}$×（5-2t）×$\frac{3}{2}$=-$\frac{3}{2}$t+$\frac{15}{4}$，
如图2，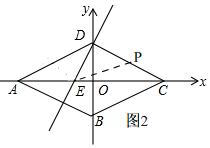

点P在DC边上运动时，即$\frac{5}{2}$＜t≤5时，
S=$\frac{1}{2}$PD×DE=$\frac{1}{2}$×（2t-5）×$\frac{5}{2}$=$\frac{5}{2}$t-$\frac{25}{4}$；
∴S=$\left\{\begin{array}{l}{-\frac{3}{2}t+\frac{15}{4}（0≤t＜\frac{5}{2}）}\\{\frac{5}{2}t-\frac{25}{4}（\frac{5}{2}＜t≤5）}\end{array}\right.$，
（3）设BP与AC相交于点Q，
在菱形ABCD中，∠DAB=∠DCB，DE⊥DC，
∴DE⊥AB，
∴∠DAB+∠ADE=90°，
∴∠DCB+∠ADE=90°，
∴要使∠EPD+∠DCB=90°，
∴∠EPD=∠ADE，
当点P在AD上运动时，如图3，

∵∠EPD=∠ADE，
∴EF垂直平分线PD，
∴AP=AD-2DF=AD-2$\sqrt{D{E}^{2}-E{F}^{2}}$，
∴2t=5-$\sqrt{\frac{25}{4}-\frac{9}{4}}$，
∴t=$\frac{1}{2}$，
此时AP=1，
∵AP∥BC，
∴△APQ∽△CBQ，
∴$\frac{AQ}{CQ}=\frac{AP}{BC}$，
∴$\frac{AQ}{AC-AQ}=\frac{AP}{BC}$，
∴$\frac{AQ}{4\sqrt{5}-AQ}=\frac{1}{5}$，
∴AQ=$\frac{2\sqrt{5}}{3}$，
∴OQ=OA-AQ=$\frac{4\sqrt{5}}{3}$，
在Rt△OBQ中，tan∠OQB=$\frac{OB}{OQ}$=$\frac{\sqrt{5}}{\frac{4\sqrt{5}}{3}}$=$\frac{3}{4}$，
当点P在DC上运动时，如图4，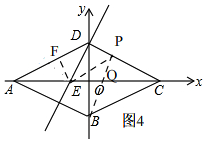

∵∠EPD=∠ADE，∠EDP=∠EFD=90°
∴△EDP∽△EFD，
∴$\frac{DP}{DF}=\frac{DE}{EF}$，
∴DP=$\frac{DE×DF}{EF}$=$\frac{\frac{5}{2}×\sqrt{\frac{25}{4}-\frac{9}{4}}}{\frac{3}{2}}$=$\frac{10}{3}$，
∴2t=AD-DP=5+$\frac{10}{3}$，
∴t=$\frac{25}{6}$，
此时CP=DC-DP=5-$\frac{10}{3}$=$\frac{5}{3}$，
∵PC∥AB，
∴△CPQ∽△ABQ，
∴$\frac{CQ}{AQ}=\frac{CP}{AB}$，
∴$\frac{CQ}{AC-CQ}=\frac{CP}{AB}$，
∴$\frac{CQ}{4\sqrt{5}-CQ}=\frac{1}{3}$，
∴CQ=$\sqrt{5}$，
∴OQ=OC-CQ=2$\sqrt{5}$-$\sqrt{5}$=$\sqrt{5}$，
在Rt△OBD中，tan∠OQB=$\frac{OB}{OQ}$=$\frac{\sqrt{5}}{\sqrt{5}}$=1，
即：当t=$\frac{1}{2}$时，∠EPD+∠DCB=90°．此时直线BP与直线AC所夹锐角的正切值为$\frac{3}{4}$．
当t=$\frac{25}{6}$时，∠EPD+∠DCB=90°．此时直线BP与直线AC所夹锐角的正切值为1．

点评 此题是一次函数综合题，主要考查菱形的性质，待定系数法求直线解析式，相似三角形的判定和性质，找出相似三角形是解本题的关键，分情况讨论是解本题的难点．