
分析 (1)根据整式的运算法则即可求出答案.
(2)先化简A-2B,然后求出a与b的值,最后将a、b的值代入原式即可求出答案.
解答 解:(1)由题意可知:
B=-ab2-[-a2b-2(2ab2-a2b)]
=-ab2-(-a2b-4ab2+2a2b)
=-ab2-(-4ab2+a2b)
=-ab2+4ab2-a2b
=3ab2-a2b
(2)由题意可知:a=1,b=-2
A-2B=-a2b-2(2ab2-a2b)-2(3ab2-a2b)
=-a2b-4ab2+2a2b-6ab2+2a2b
=-4ab2+a2b-6ab2+2a2b
=-10ab2+3a2b
=-10×1×4+3×1×(-2)
=-40-6
=-46
点评 本题考查整式的运算,解题的关键是熟练运用整式的运算法则,本题属于基础题型.


科目:初中数学 来源: 题型:选择题
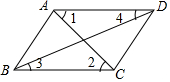 如图,下列条件中,不能判定AD∥BC的是( )
如图,下列条件中,不能判定AD∥BC的是( )| A. | ∠1=∠2 | B. | ∠3=∠4 | C. | ∠ADC+∠DCB=180° | D. | ∠BAD+∠ADC=180° |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
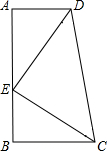 如图,在梯形ABCD中,AD∥BC,∠A=90°,点E在边AB上,AD=BE,AE=BC,由此可以知道△ADE旋转后能与△BEC重合,那么旋转中心是CD的中点.
如图,在梯形ABCD中,AD∥BC,∠A=90°,点E在边AB上,AD=BE,AE=BC,由此可以知道△ADE旋转后能与△BEC重合,那么旋转中心是CD的中点.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
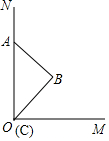 已知OM⊥ON,斜边长为4的等腰直角△ABC的斜边AC在射线上,顶点C与O重合,若点A沿NO方向向O运动,△ABC的顶点C随之沿OM方向运动,点A移动到点O为止,则直角顶点B运动的路径长是8-4$\sqrt{2}$.
已知OM⊥ON,斜边长为4的等腰直角△ABC的斜边AC在射线上,顶点C与O重合,若点A沿NO方向向O运动,△ABC的顶点C随之沿OM方向运动,点A移动到点O为止,则直角顶点B运动的路径长是8-4$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 等腰三角形 | B. | 等边三角形 | C. | 等腰直角三角形 | D. | 直角三角形 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ($\sqrt{6}$)2=±6 | B. | ($\sqrt{-7}$)2=-7 | C. | $\sqrt{3}$×$\sqrt{6}$=3$\sqrt{2}$ | D. | $\sqrt{6}$÷$\sqrt{3}$=3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com