
 等腰直角三角形ABC,∠ABC=90°,AB=2,O为AC中点,∠EOF=45°,求△BEF的周长.
等腰直角三角形ABC,∠ABC=90°,AB=2,O为AC中点,∠EOF=45°,求△BEF的周长. 分析 过点O作OD⊥OF,依据等腰直角三角形的性质可得到OB=AO,∠OBF=∠OAD=45°,然后依据同角的余角相等可证明∠AOD=∠BOF,然后依据ASA可证明△AOD≌△BOF,于是得到BF=AD,然后再证明△DOE≌△FOE,依据全等三角形的性质可得到DE=EF,最后将△EFB的周长转化为AB的长求解即可.
解答 解:如图所示:过点O作OD⊥OF.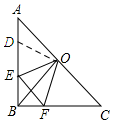
∵△ABC为等腰直角三角形,O为斜边AC的中点,
∴OB⊥AC,∠A=∠C=45°,∠OBF=$\frac{1}{2}$∠ABC=45°,∠BOA=90°,OB=AO,
∴∠OBF=∠OAD,∠BOD+∠DOA=90°.
∵OD⊥OF,
∴∠DOB+∠BOF=90°.
∴∠AOD=∠BOF.
在△AOD和△BOF中$\left\{\begin{array}{l}{∠OBF=∠OAD}\\{OB=AO}\\{∠AOD=∠BOF}\end{array}\right.$,
∴△AOD≌△BOF.
∴BF=AD,OD=OF.
∵∠DOF=90°,∠EOF=45°,
∴∠DOE=∠FOE=45°.
在△DOE和△FOE中$\left\{\begin{array}{l}{OD=OF}\\{∠DOE=∠FOE}\\{OE=OE}\end{array}\right.$,
∴△DOE≌△FOE.
∴DE=EF.
∴△EFB的周长=BE+FB+EF=BE+AD+DE=AB=2.
点评 本题主要考查的是全等三角形的性质和判定、等腰直角三角形的性质,将△EFB的周长转化为AB的长是解题的关键.


 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:填空题
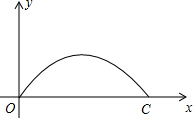 如图,济南建邦大桥有一段抛物线型的拱梁,抛物线的表达式为y=ax2+bx,小强骑自行车从拱梁一端O匀速穿过拱梁部分的桥面OC,当小强骑自行车行驶8秒时和24秒时拱梁的高度相同,则小强骑自行车通过拱梁部分的桥面OC共需32秒.
如图,济南建邦大桥有一段抛物线型的拱梁,抛物线的表达式为y=ax2+bx,小强骑自行车从拱梁一端O匀速穿过拱梁部分的桥面OC,当小强骑自行车行驶8秒时和24秒时拱梁的高度相同,则小强骑自行车通过拱梁部分的桥面OC共需32秒.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
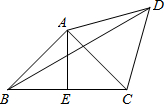 如图,四边形ABCD中,AB=AC=AD,E是BC的中点,AE=CE,∠BAC=3∠CBD,BD=6$\sqrt{2}$+6$\sqrt{6}$,则AB的长为( )
如图,四边形ABCD中,AB=AC=AD,E是BC的中点,AE=CE,∠BAC=3∠CBD,BD=6$\sqrt{2}$+6$\sqrt{6}$,则AB的长为( )| A. | 6 | B. | 6$\sqrt{2}$ | C. | 12 | D. | 10$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | AB=A'C' | B. | BC=B'C' | C. | AC=B'C' | D. | ∠A=∠A' |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
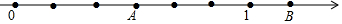
| A. | $1\frac{1}{3}$ | B. | $1\frac{1}{4}$ | C. | $1\frac{1}{5}$ | D. | $1\frac{1}{6}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
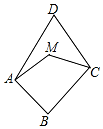 如图,M是线段AD、CD的垂直平分线交点,AB⊥BC,∠D=55°,则∠MAB+∠MCB的大小是( )
如图,M是线段AD、CD的垂直平分线交点,AB⊥BC,∠D=55°,则∠MAB+∠MCB的大小是( )| A. | 120° | B. | 130° | C. | 140° | D. | 160° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com