
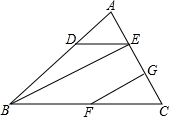
 完成下面的证明:
完成下面的证明:科目:初中数学 来源: 题型:选择题
| A. | $\frac{8000}{x}$-$\frac{8000}{x+10}$=40 | B. | $\frac{8000}{x+10}$-$\frac{8000}{x}$=40 | ||
| C. | $\frac{8000}{x-10}$=$\frac{8000}{x}$+40 | D. | $\frac{8000}{x-10}$=$\frac{8000}{x}$-40 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
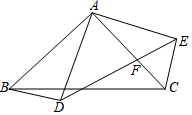 如图△ABC与△ADE都是以A为直角顶点的等腰直角三角形,DE交AC于点F.
如图△ABC与△ADE都是以A为直角顶点的等腰直角三角形,DE交AC于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
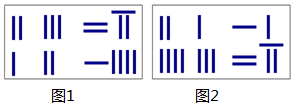 《九章算术》是我国东汉初年编订的一部数学经典著作.在它的“方程”一章里,一次方程组是由算筹布置而成的.《九章算术》中的算筹图是竖排的,现在我们把它改为横排,如图1、图2.图中各行从左到右列出的算筹数分别表示未知数x,y的系数与相应的常数项.把图1所示的算筹图用我们现在所熟悉的方程组形式表述出来,就是$\left\{\begin{array}{l}{2x+3y=27}\\{x+2y=14}\end{array}\right.$,类似地,图2所示的算筹图我们可以表述为( )
《九章算术》是我国东汉初年编订的一部数学经典著作.在它的“方程”一章里,一次方程组是由算筹布置而成的.《九章算术》中的算筹图是竖排的,现在我们把它改为横排,如图1、图2.图中各行从左到右列出的算筹数分别表示未知数x,y的系数与相应的常数项.把图1所示的算筹图用我们现在所熟悉的方程组形式表述出来,就是$\left\{\begin{array}{l}{2x+3y=27}\\{x+2y=14}\end{array}\right.$,类似地,图2所示的算筹图我们可以表述为( )| A. | $\left\{\begin{array}{l}{2x+y=16}\\{4x+3y=22}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{2x+y=16}\\{4x+3y=27}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{2x+y=11}\\{4x+3y=27}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{2x+y=11}\\{4x+3y=22}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com