
【题目】某学校为了解学生的课外阅读情况,随机抽取了50名学生,并统计他们平均每天的课外阅读时间t(单位:min),然后利用所得数据绘制成如下不完整的统计表.
课外阅读时间t | 频数 | 百分比 |
10≤t<30 | 4 | 8% |
30≤t<50 | 8 | 16% |
50≤t<70 | a | 40% |
70≤t<90 | 16 | b |
90≤t<110 | 2 | 4% |
合计 | 50 | 100% |
请根据图表中提供的信息回答下列问题:
(1)a= ,b= ;
(2)将频数分布直方图补充完整;
(3)若全校有900名学生,估计该校有多少学生平均每天的课外阅读时间不少于50min?

科目:初中数学 来源: 题型:
【题目】如图,一个长方形运动场被分割成 A、B、A、B、C 共 5 个区域,A 区域是边长为 a 米的正方形,C 区是边长为 c 米的正方形
(1)列式表示一个 B 区长方形场地的周长,并将式子化简;
(2)列式表示整个长方形运动场的周长,并将式子化简;
(3)当a=4,c=2时,求运动场地的周长和面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场投入13 800元资金购进甲、乙两种矿泉水共500箱,矿泉水的成本价和销售价如表所示:
类别/单价 | 成本价 | 销售价(元/箱) |
甲 | 24 | 36 |
乙 | 33 | 48 |
(1)该商场购进甲、乙两种矿泉水各多少箱?
(2)全部售完500箱矿泉水,该商场共获得利润多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE=90°。

①当点D在AC上时,如图1,线段BD、CE有怎样的数量关系和位置关系?写出你猜想的结论,并说明理由;
②将图1中的△ADE绕点A顺时针旋转α角(0°<α<90°),如图2,线段BD、CE有怎样的数量关系和位置关系?请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=﹣2x+10与x轴,y轴相交于A,B两点,点C的坐标是(8,4),连接AC,BC.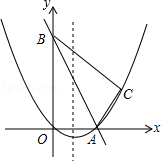
(1)求过O,A,C三点的抛物线的解析式,并判断△ABC的形状;
(2)动点P从点O出发,沿OB以每秒2个单位长度的速度向点B运动;同时,动点Q从点B出发,沿BC以每秒1个单位长度的速度向点C运动.规定其中一个动点到达端点时,另一个动点也随之停止运动.设运动时间为t秒,当t为何值时,PA=QA?
(3)在抛物线的对称轴上,是否存在点M,使以A,B,M为顶点的三角形是等腰三角形?若存在,求出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国最大的水果公司“佳沃鑫荣懋”旗下子公司“欢乐果园”购进某种水果的成本为20元/kg,经过市场调研发现,这种水果在未来48天的销售单价p(元/kg)与时间t(天)之间的函数关系式为P= 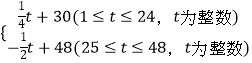 ,且其日销售量y(kg)与时间t(天)的关系如表:
,且其日销售量y(kg)与时间t(天)的关系如表:
时间t(天) | 1 | 3 | 6 | 10 | 20 | 40 | … |
日销售量y(kg) | 118 | 114 | 108 | 100 | 80 | 40 | … |
(1)已知y与t之间的变化规律符合一次函数关系,试求在第30天的日销售量是多少?
(2)问哪一天的销售利润最大?最大日销售利润为多少?
(3)在实际销售前24天中,子公司决定每销售1kg水果就捐赠n元利润(n<9)给“精准扶贫”对象.现发现:在前24天中,每天扣除捐赠后的日销售利润随时间t的增大而增大,求n的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com