
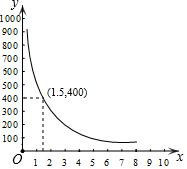
 码头工人往一艘轮船上装载货物,装完货物所需时间y(min)与装载速度x(t/min)之间的函数关系如图.
码头工人往一艘轮船上装载货物,装完货物所需时间y(min)与装载速度x(t/min)之间的函数关系如图.分析 (1)根据函数图象可以设出函数的解析式,然后根据图象中的数据即可求得函数的解析式;
(2)根据函数图象中的数据可以求得这批货的质量;
(3)根据题意可以列出相应的分式方程,从而可以解答本题.
解答 解:(1)设y与x的函数关系式是y=$\frac{k}{x}$,
400=$\frac{k}{1.5}$,得k=600,
即y与x的函数关系式是y=$\frac{600}{x}$;
(2)由题意可得,
这批货物的质量是:1.5×400=600(t),
答:这批货物的质量是600t;
(3)设原定速度为mt/min,
$\frac{600}{m}-20=\frac{600}{1.2m}$,
解得,m=5,
经检验m=5是原分式方程的解,
答:原定速度每分钟卸货5吨.
点评 本题考查反比例函数的应用,解答本题的关键是求出相应的函数解析式,列出相应的方程,注意分式方程要检验.


 英才计划期末调研系列答案
英才计划期末调研系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 计费项目 | 里程费 | 时长费 | 远途费 |
| 单价 | 1.8元/公里 | 0.3元/分钟 | 0.8元/公里 |
| 注:车费由里程费、时长费、远途费三部分构成,其中里程费按行车的实际里程计算;时长费按行车的实际时间计算;远途费的收取方式为:行车里程7公里以内(含7公里)不收远途费,超过7公里的,超出部分每公里收0.8元. | |||
| A. | 10分钟 | B. | 13分钟 | C. | 15分钟 | D. | 19分钟 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
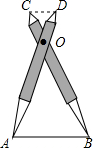 如图,比例规是一种画图工具,它由长度相等的两脚AD和BC交叉构成,利用它可以把线段按一定的比例伸长或缩短.如果把比例规的两脚合上,使螺丝钉固定在刻度4的地方(即同时使OA=4OD,OB=4OC),然后张开两脚,使A,B两个尖端分别在线段l的两个端点上,若CD=3,则AB的长是( )
如图,比例规是一种画图工具,它由长度相等的两脚AD和BC交叉构成,利用它可以把线段按一定的比例伸长或缩短.如果把比例规的两脚合上,使螺丝钉固定在刻度4的地方(即同时使OA=4OD,OB=4OC),然后张开两脚,使A,B两个尖端分别在线段l的两个端点上,若CD=3,则AB的长是( )| A. | 12 | B. | 9 | C. | 8 | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (a2+2b2)-2(-a2+b2)=3a2+b2 | B. | $\frac{{a}^{2}+1}{a-1}$-a-1=$\frac{2a}{a-1}$ | ||
| C. | (-a)3m÷am=(-1)ma2m | D. | 6x2-5x-1=(2x-1)(3x-1) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
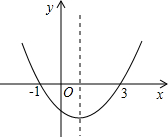 如图,抛物线y=ax2+bx+c(a≠0)的开口向上,与x轴交点的横坐标分别为-1、3,则下列说法错误的是( )
如图,抛物线y=ax2+bx+c(a≠0)的开口向上,与x轴交点的横坐标分别为-1、3,则下列说法错误的是( )| A. | 对称轴是直线x=1 | B. | 方程ax2+bx+c=0的解是x1=-1,x2=3 | ||
| C. | 当x<1,y随x的增大而增大 | D. | 当-1<x<3时,y<0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com