
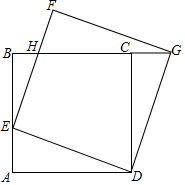
 ��ͼ��������ABCD�ı߳�Ϊ2������E�ӵ�A�������ر�AB-BC���յ�C�˶�����DEΪ����������DEFG����D��E��F��G��˳ʱ�뷽�����У������E�˶����ٶ�Ϊÿ��1����λ���˶���ʱ��Ϊx �룮
��ͼ��������ABCD�ı߳�Ϊ2������E�ӵ�A�������ر�AB-BC���յ�C�˶�����DEΪ����������DEFG����D��E��F��G��˳ʱ�뷽�����У������E�˶����ٶ�Ϊÿ��1����λ���˶���ʱ��Ϊx �룮���� ��1���������ε����ʵó�AD=CD��DE=DG����ADE+��EDC=��EDC+��CDG=90�㣬֤����ADE=��CDG����SAS֤����ADE�ա�CDG���ó���DCG=��DAE=90�㣬֤����DCG+��DCB=180�㣬���ɵó����ۣ�
��2����������ۣ��ٵ���E��AB����ʱ������E��EK��AD����CD�ڵ�K����AC��EK��AD��֤����ADE�ס�BEH�������������ε����ʵó�$\frac{AD}{BE}$=$\frac{AE}{BH}$�����BH=$\frac{x��2-x��}{2}$��S=������ABCD�����-��ADE�����-��BEH����������ɵó������
�ڵ���E��BC����ʱ��S=��DEC�����=4-x��
��3���ɣ�1��֪������E��AB��ʱ����G��ֱ��BC�ϣ�����E��B���غ�ʱ����F��λ����ͼ2��ʾ����F�˶���·��ΪBF��ͬ������E��BC��ʱ������E��C���غ�ʱ����F�˶���·��ΪFG���ɹ��ɶ������BD�����ɵó������
��� ��1��֤�������ı���ABCD���ı���DEFG���������Σ�
��AD=CD��DE=DG����ADE+��EDC=��EDC+��CDG=90�㣬
���ADE=��CDG��
�ڡ�ADE�͡�CDG�У�$\left\{\begin{array}{l}{AD=CD}\\{��ADE=��CDG}\\{DE=DG}\end{array}\right.$��
���ADE�ա�CDG ��SAS����
���DCG=��DAE=90�㣬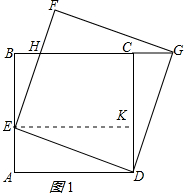
�ߡ�DCB=90�㣬
���DCG+��DCB=180�㣬
���G��ֱ��BC�ϣ�
��2���⣺�ٵ���E��AB����ʱ������E��EK��AD����CD�ڵ�K����ͼ1��ʾ��
��AC��EK��AD��
���HEK=��EHB����DEK=��EDA��
�ߡ�EHB+��BEH=90�㣬��EDA+��AED=90�㣬��HEK+��DEK=90�㣬
���EDA=��BEH����AED=��EHB��
���ADE�ס�BEH��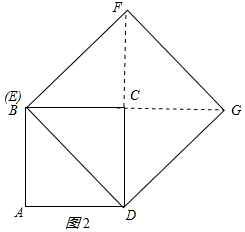
��$\frac{AD}{BE}$=$\frac{AE}{BH}$����$\frac{2}{2-x}$=$\frac{x}{BH}$��
��BH=$\frac{x��2-x��}{2}$��
S=������ABCD�����-��ADE�����-��BEH�����=2��2-$\frac{1}{2}$��2��x-$\frac{1}{2}$����2-x����$\frac{x��2-x��}{2}$=$\frac{-{x}^{3}+4{x}^{2}-8x+16}{4}$��
�ڵ���E��BC����ʱ��S=��DEC�����=$\frac{1}{2}$��2����4-x��=4-x��
��3���⣺�ɣ�1��֪������E��AB��ʱ����G��ֱ��BC�ϣ�����E��B���غ�ʱ����F��λ����ͼ2��ʾ��
��F�˶���·��ΪBF��
ͬ������E��BC��ʱ������E��C���غ�ʱ����F�˶���·��ΪFG��
��BD=$\sqrt{A{D}^{2}+A{B}^{2}}$=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$��
��BF+FG=2BD=4$\sqrt{2}$��
���F�˶���·����Ϊ4$\sqrt{2}$��
���� �������ı����ۺ���Ŀ�������������ε����ʡ�ƽ���ߵ��ж������ʡ�����������ļ��㡢ȫ�������ε��ж������ʡ����������ε��ж������ʡ����ɶ�����֪ʶ���������������ε����ʡ�ȫ�������ε��ж������ʡ����������ε��ж��������ǽ������Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 19cm��11cm | B�� | 19cm��14cm | C�� | 11cm ��14cm | D�� | 19cm |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3 �� | B�� | 4�� | C�� | 5�� | D�� | 6�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | -2 | C�� | 1 | D�� | -1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����A��B��C��D�ڡ�O�ϣ���O�ڡ�D���ڲ����ı���OABCΪƽ���ı��Σ����B=120�㣮
��ͼ����A��B��C��D�ڡ�O�ϣ���O�ڡ�D���ڲ����ı���OABCΪƽ���ı��Σ����B=120�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����

| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 10��51 | B�� | 10��21 | C�� | 10��15 | D�� | 15��01 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com