
 如图,已知矩形ABCD,AD=9,AB=6,若点G、H、M、N分别在AB、CD、AD、BC上,线段MN与GH交于点K.若∠GKM=45°,NM=3$\sqrt{5}$,则GH=3$\sqrt{10}$.
如图,已知矩形ABCD,AD=9,AB=6,若点G、H、M、N分别在AB、CD、AD、BC上,线段MN与GH交于点K.若∠GKM=45°,NM=3$\sqrt{5}$,则GH=3$\sqrt{10}$. 分析 过点A作AE∥GH交CD于E,作AF∥MN交BC于F,于是得到AF=MN=3$\sqrt{5}$,AE=GH,由于∠GKM=45°,得到∠BAF+∠DAE=90°-45°=45°,作∠QAE=45°交CD的延长线于Q,推出∠QAD+∠DAE=45°,通过△ABF≌△AQD,根据相似三角形的性质得到$\frac{AB}{AD}=\frac{AF}{AQ}$,求得AQ=$\frac{9\sqrt{5}}{2}$,在Rt△ADQ中,由勾股定理得到DQ=$\sqrt{A{Q}^{2}-A{D}^{2}}$=$\frac{9}{2}$,过点E作EP⊥AQ于P,得到△AEP是等腰直角三角形,设GH=AE=x,则AP=EP=$\frac{\sqrt{2}}{2}$AE=$\frac{\sqrt{2}}{2}$,然后利用∠Q的正切值列出方程求解即可.
解答  解:如图,过点A作AE∥GH交CD于E,作AF∥MN交BC于F,
解:如图,过点A作AE∥GH交CD于E,作AF∥MN交BC于F,
则AF=MN=3$\sqrt{5}$,AE=GH,
∵∠GKM=45°,
∴∠BAF+∠DAE=90°-45°=45°,
作∠QAE=45°交CD的延长线于Q,
则∠QAD+∠DAE=45°,
∴∠QAD=∠FAB,
∵∠B=∠ADQ=90°,
∴△ABF∽△AQD,
∴$\frac{AB}{AD}=\frac{AF}{AQ}$,
∴$\frac{6}{9}=\frac{3\sqrt{5}}{AQ}$,
∴AQ=$\frac{9\sqrt{5}}{2}$,
在Rt△ADQ中,DQ=$\sqrt{A{Q}^{2}-A{D}^{2}}$=$\frac{9}{2}$,
过点E作EP⊥AQ于P,
∵∠QAE=45°,
∴△AEP是等腰直角三角形,
设GH=AE=x,则AP=EP=$\frac{\sqrt{2}}{2}$AE=$\frac{\sqrt{2}}{2}$x,
∵tan∠Q=$\frac{AD}{DQ}$=$\frac{PE}{PQ}$,
∴$\frac{9}{\frac{9}{2}}$=$\frac{\frac{\sqrt{2}}{2}x}{\frac{9\sqrt{5}}{2}-\frac{\sqrt{2}}{2}x}$,
解得x=3$\sqrt{10}$,
所以GH=3$\sqrt{10}$.
故答案为:3$\sqrt{10}$.
点评 本题考查了矩形的性质,相似三角形的判定和性质,等腰直角三角形的性质,锐角三角函数的定义,熟记各性质并作辅助线构造出相似三角形和等腰直角三角形是解题的关键.


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:初中数学 来源: 题型:解答题
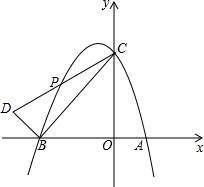 如图,抛物线y=-$\frac{1}{2}$x2+bx+4与x轴交于A(2,0)、B两点,与y轴交于点C.
如图,抛物线y=-$\frac{1}{2}$x2+bx+4与x轴交于A(2,0)、B两点,与y轴交于点C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
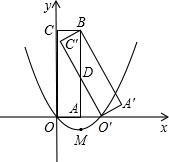 如图,矩形A′BC′O′是矩形OABC(边OA在x轴正半轴上,边OC在y轴正半轴上)绕B点逆时针旋转得到的,O′点在x轴的正半轴上,B点的坐标为(1,3).
如图,矩形A′BC′O′是矩形OABC(边OA在x轴正半轴上,边OC在y轴正半轴上)绕B点逆时针旋转得到的,O′点在x轴的正半轴上,B点的坐标为(1,3).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图是“温州南”动车站前广场设计方案之一,其中大广场地面长方形的长200米,宽100米,大广场“含”一个边长为80米正方形广场,正方形广场又“含”一个半径为40米的圆形中心广场,按设计,图中阴影处铺设某种广场地砖.则广场地砖需要铺多少平方米?(π取3,结果精确到千位)
如图是“温州南”动车站前广场设计方案之一,其中大广场地面长方形的长200米,宽100米,大广场“含”一个边长为80米正方形广场,正方形广场又“含”一个半径为40米的圆形中心广场,按设计,图中阴影处铺设某种广场地砖.则广场地砖需要铺多少平方米?(π取3,结果精确到千位)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
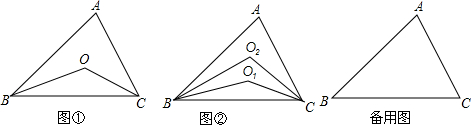
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
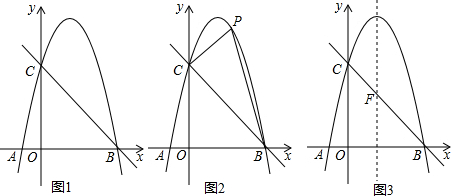
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com