
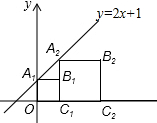
 正方形A1B1C1O和正方形A2B2C2C1按如图所示方式放置,A1、A2在直线y=2x+1上,点C1,C2在x轴上,已知A1点的坐标是(0,1),则点B2的坐标为(4,3).
正方形A1B1C1O和正方形A2B2C2C1按如图所示方式放置,A1、A2在直线y=2x+1上,点C1,C2在x轴上,已知A1点的坐标是(0,1),则点B2的坐标为(4,3). 分析 根据正方形的性质以及点A1的坐标即可得出OC1的长度,将x=1代入y=2x+1中求出y值,再根据正方形的性质即可得出C1C2=B2C2=3,由此即可得出点B2的坐标.
解答 解:∵A1点的坐标是(0,1),四边形A1B1C1O为正方形,
∴OC1=1,
令y=2x+1中x=1,则y=3,
∴C1A2=3,
∵四边形A2B2C2C1为正方形,
∴C1C2=B2C2=3,
∴OC2=OC1+C1C2=4,
∴点B2的坐标为(4,3).
故答案为:(4,3).
点评 本题考查了一次函数图象上点的坐标特征以及正方形的性质,解题的关键是求出线段OC1、C1C2、B2C2的长度.本题属于基础题,难度不大,解决该题型题目时,根据正方形的性质找出边的长度是关键.


科目:初中数学 来源: 题型:选择题
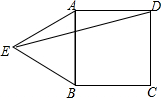 如图,点E是正方形ABCD外一点,EA=4,EB=3,且∠AEB=45°,则ED的长为( )
如图,点E是正方形ABCD外一点,EA=4,EB=3,且∠AEB=45°,则ED的长为( )| A. | $\sqrt{23}$ | B. | 2$\sqrt{10}$ | C. | $\sqrt{41}$ | D. | 5$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{5}×\sqrt{7}$=2$\sqrt{3}$ | B. | $\sqrt{6}÷\sqrt{3}$=$\sqrt{2}$ | C. | $\sqrt{\frac{1}{10}}$×$\sqrt{8}$=$\frac{2\sqrt{5}}{5}$ | D. | $\sqrt{\frac{4}{7}}$÷$\sqrt{\frac{7}{4}}$=$\frac{4}{7}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
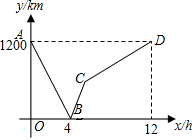 如图所示,一列列车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km)图中的折线表示y与x之间的函数关系,下列说法中错误的是( )
如图所示,一列列车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km)图中的折线表示y与x之间的函数关系,下列说法中错误的是( )| A. | B点表示快车与慢车出发4小时两车相遇 | |
| B. | B-C-D段表示慢车先加速后减速最后到达甲地 | |
| C. | 快车的速度为200km/h | |
| D. | 慢车的速度为100km/h |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com