
| A. | $\frac{1-x}{x-1}$ | B. | $\frac{{x}^{2}-1}{{x}^{2}+2x+1}$ | C. | $\frac{x-y}{{x}^{2}+{y}^{2}}$ | D. | -$\frac{13{m}^{2}}{2m}$ |
分析 要判断分式是否是最简分式,只需判断它能否化简,不能化简的即为最简分式.
解答 解:A、原式=-$\frac{1-x}{1-x}$=-1,不是最简分式,故本选项错误;
B、原式=$\frac{(x+1)(x-1)}{(x+1)^{2}}$=$\frac{x-1}{x+1}$,不是最简分式,故本选项错误;
C、该分式是最简分式,故本选项正确;
D、原式=-$\frac{13m}{2}$,不是最简分式,故本选项错误;
故选:C.
点评 此题考查了最简分式的判断,当分式的分子分母中除1以外再没有其他的公因式时,此时分式成为最简分式,一般情况下分式若不是最简分式,应将分子分母中的公因式约分后得到最简结果.掌握最简分式的判断方法是解本题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B. | 2$\sqrt{2}$-$\sqrt{2}$=$\sqrt{2}$ | C. | $\sqrt{(-4)×(-9)}$=$\sqrt{-4}$×$\sqrt{-9}$ | D. | $\sqrt{6}$÷$\sqrt{3}$=$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
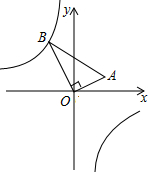 如图,在△AOB中,∠AOB=90°,点A的坐标为(2,1),BO=2$\sqrt{5}$,反比例函数y=$\frac{k}{x}$的图象经过点B,则k的值为-8.
如图,在△AOB中,∠AOB=90°,点A的坐标为(2,1),BO=2$\sqrt{5}$,反比例函数y=$\frac{k}{x}$的图象经过点B,则k的值为-8.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在边长为1个单位长度的小正方形组成的网格中,△ABC的顶点A,B,C在小正方形的顶点上.以点O为坐标原点建立平面直角坐标系,请回答下列问题:
如图,在边长为1个单位长度的小正方形组成的网格中,△ABC的顶点A,B,C在小正方形的顶点上.以点O为坐标原点建立平面直角坐标系,请回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com