
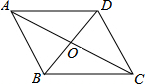
 如图,AB∥CD,AD∥BC,AC与BD交于点O,那么图中全等的三角形共有4对.
如图,AB∥CD,AD∥BC,AC与BD交于点O,那么图中全等的三角形共有4对. 分析 由条件可得四边形ABCD为平行四边形,可得到AO=OC,BO=DO,可证得△AOD≌△COB,△AOB≌△COD,由平行线的性质可得到∠BAC=∠DCA,∠BCA=∠DAC,可证明△ABC≌△CDA,同理可证明△ABD≌△CDB,可得答案.
解答 解:
∵AB∥CD,AD∥BC,
∴OA=OC,OB=OD,
在△AOD和△COB中
$\left\{\begin{array}{l}{OA=OC}\\{∠AOD=∠BOC}\\{OD=OB}\end{array}\right.$
∴△AOD≌△COB(SAS),
同理可证明△AOB≌△COD,
∵AB∥CD,AD∥BC,
∴∠BAC=∠DCA,∠BCA=∠DAC,
在△ABC和△CDA中,
$\left\{\begin{array}{l}{∠BAC=∠DCA}\\{AC=CA}\\{∠BCA=∠DAC}\end{array}\right.$
△ABC≌△CDA(ASA),
同理可证明△ABD≌△CDB,
∴共有4对三角形全等,
故答案为:4.
点评 本题主要考查全等三角形的判定,利用条件证明四边形ABCD为平行四边形是解题的关键.


科目:初中数学 来源: 题型:解答题
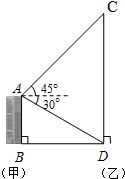 如图,甲楼AB的高度为50米,自甲楼楼顶A处,测得乙楼顶端C处的仰角为45°,测得乙楼底部D处的俯角为30°,求乙楼CD的高度(结果精确到1米,$\sqrt{3}$取1.73).
如图,甲楼AB的高度为50米,自甲楼楼顶A处,测得乙楼顶端C处的仰角为45°,测得乙楼底部D处的俯角为30°,求乙楼CD的高度(结果精确到1米,$\sqrt{3}$取1.73).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 决赛成绩(单位:分) | |
| 七年级 | 80 86 88 80 88 99 80 74 91 89 |
| 八年级 | 85 85 87 97 85 76 88 77 87 88 |
| 九年级 | 82 80 78 78 81 96 97 88 89 86 |
| 平均数 | 众数 | 中位数 | |
| 七年级 | 85.5 | 87 | |
| 八年级 | 85.5 | 85 | |
| 九年级 | 84 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在如图所示网格内建立恰当直角坐标系后,画出函数y=x2和y=-$\frac{1}{2}$x2的图象,并根据图象回答下列问题(设小方格的边长为1):
在如图所示网格内建立恰当直角坐标系后,画出函数y=x2和y=-$\frac{1}{2}$x2的图象,并根据图象回答下列问题(设小方格的边长为1):查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com