
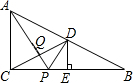
 如图,在Rt△ABC中,∠ACB=90°,点D是AB边的中点,过D作DE⊥BC于点E,点P是边BC上的一个动点,AP与CD相交于点Q.当AP+PD的值最小时,AQ与PQ之间的数量关系是( )
如图,在Rt△ABC中,∠ACB=90°,点D是AB边的中点,过D作DE⊥BC于点E,点P是边BC上的一个动点,AP与CD相交于点Q.当AP+PD的值最小时,AQ与PQ之间的数量关系是( )| A. | AQ=$\frac{5}{2}$PQ | B. | AQ=3PQ | C. | AQ=$\frac{8}{3}$PQ | D. | AQ=4PQ |
分析 如图,作点A关于BC的对称点A′,连接A′D交BC于点P,此时PA+PD最小.作DM∥BC交AC于M,交PA于N,利用平行线的性质,证明AN=PN,利用全等三角形证明NQ=PQ,即可解决问题.
解答 解:如图,作点A关于BC的对称点A′,连接A′D交BC于点P,此时PA+PD最小.作DM∥BC交AC于M,交PA于N.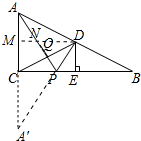 ∵∠ACB=∠DEB=90°,
∵∠ACB=∠DEB=90°,
∴DE∥AC,
∵AD=DB,
∴CE=EB,
∴DE=$\frac{1}{2}$AC=$\frac{1}{2}$CA′,
∵DE∥CA′,
∴$\frac{EP}{PC}$=$\frac{DE}{CA′}$=$\frac{1}{2}$,
∵DM∥BC,AD=DB,
∴AM=MC,AN=NP,
∴DM=$\frac{1}{2}$BC=CE=EB,MN=$\frac{1}{2}$PC,
∴MN=PE,ND=PC,
在△DNQ和△CPQ中,
$\left\{\begin{array}{l}{∠NDQ=∠QCP}\\{∠NQD=∠PQC}\\{DN=PC}\end{array}\right.$,
∴△DNQ≌△CPQ,
∴NQ=PQ,
∵AN=NP,
∴AQ=3PQ.
故选B.
点评 本题考查轴对称最短问题、全等三角形的判定和性质、平行线分线段成比例定理等知识,解题的关键是利用对称找到点P位置,熟练掌握平行线的性质,属于中考常考题型.


 优生乐园系列答案
优生乐园系列答案科目:初中数学 来源: 题型:选择题
 二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论;①2a+b>0;②abc<0;③b2-4ac>0;④a+b+c<0;⑤4a-2b+c<0;⑥若(x1,y1)、(x2,y2)在函数图象上,当x1<x2<1时,y1<y2,其中正确的个数是( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论;①2a+b>0;②abc<0;③b2-4ac>0;④a+b+c<0;⑤4a-2b+c<0;⑥若(x1,y1)、(x2,y2)在函数图象上,当x1<x2<1时,y1<y2,其中正确的个数是( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
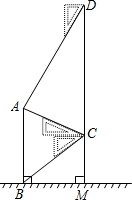 如图,某中学在教学楼前新建了一座雕塑AB.为了测量雕塑的高度,小明在二楼找到一点C,利用三角尺测得雕塑顶端点A的仰角为30°,底部点B的俯角为45°,小华在五楼找到一点D,利用三角尺测得点A的俯角为60°.若CD为9.6m,则雕塑AB的高度为多少?(结果精确到0.1m,参考数据:$\sqrt{3}$≈1.73).
如图,某中学在教学楼前新建了一座雕塑AB.为了测量雕塑的高度,小明在二楼找到一点C,利用三角尺测得雕塑顶端点A的仰角为30°,底部点B的俯角为45°,小华在五楼找到一点D,利用三角尺测得点A的俯角为60°.若CD为9.6m,则雕塑AB的高度为多少?(结果精确到0.1m,参考数据:$\sqrt{3}$≈1.73).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,直线y=kx过点A(1,2),直线y=-2x-5与x轴交于B点,直线y=kx与直线y=-2x-5交于C点,
如图,直线y=kx过点A(1,2),直线y=-2x-5与x轴交于B点,直线y=kx与直线y=-2x-5交于C点,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com