
【题目】如图,把Rt△ACO以O点为中心,逆时针旋转90 ,得Rt△BDO,点B坐标为(0,-3),点C坐标为(0, ![]() ),,抛物线y=-
),,抛物线y=-![]() x2+bx+c经过点A和点C
x2+bx+c经过点A和点C
(1)求b,c的值;
(2)在x轴以上的抛物线对称轴上是否存在点Q,使得△ACQ为等腰三角形?若存在,直接写出点Q的坐标;若不存在,请说明理由
(3)点P从点O出发沿x轴向负半轴运动,每秒1个单位,过点P作y轴的平行线交抛物线于点M,当t为几秒时,以M、P、O、C为顶点得四边形是平行四边形?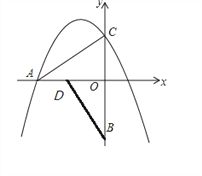
【答案】(1)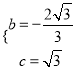 (2)存在,有2个Q点,坐标分别为:(—1,
(2)存在,有2个Q点,坐标分别为:(—1, ![]() );(—1,
);(—1, ![]() )(3)当t=2或
)(3)当t=2或![]() +1秒时,以M、P、O、C为顶点得四边形是平行四边形.
+1秒时,以M、P、O、C为顶点得四边形是平行四边形.
【解析】试题分析:(1)先由旋转得出点A的坐标为(—3,0),直接利用待定系数法求出抛物线解析式得出即可;
(2)利用当AQ=AC=![]() ,以及当AC=Q1C时,分别得出符合题意的答案即可;
,以及当AC=Q1C时,分别得出符合题意的答案即可;
(3)利用平行四边形的性质首先得出BC的长,进而表示出线段ME的长,进而求出答案.
(1) 由旋转知:OA=OB=3
∴A(—3,0)
由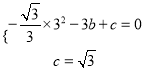 ,∴
,∴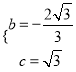 ……4分
……4分
(2)由(1)得y=-![]() x2+bx+c=-
x2+bx+c=-![]() x2
x2![]() x+
x+![]() =-
=-![]() x+1)2
x+1)2![]() ,即抛物线的对称轴为直线x=-1,
,即抛物线的对称轴为直线x=-1,
如图
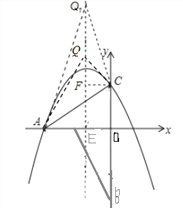
①当AC=AQ时,直线x=-1和x轴交于E点,AO=3,CO=![]() ,∴AC=
,∴AC=![]() ,AE=2,∴QE=
,AE=2,∴QE=![]() ,故Q的坐标为:(-1,
,故Q的坐标为:(-1, ![]() );
);
②当AC=Q1C时,过点C作CF⊥直线x=-1,于一点F,则FC=1,
∵AO=3,CO=![]() ,∴AC=
,∴AC=![]() ,∴Q1C=
,∴Q1C=![]() ,∴FQ1=
,∴FQ1=![]() ,故Q1的坐标为:(-1,
,故Q1的坐标为:(-1, ![]() );
);
所以存在2个Q点,坐标分别为:(—1, ![]() );(—1,
);(—1, ![]() ).
).
(3)∵OC=![]() ,当 M、P、O、C为顶点得四边形是平行四边形时,PM=
,当 M、P、O、C为顶点得四边形是平行四边形时,PM=![]()
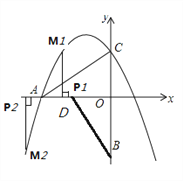
∴M点的纵坐标为![]() 或-
或-![]() .
.
由![]()
解之,x=-2或0
由 ![]()
解之,x=-1+![]() 或-1-
或-1-![]()
结合条件及图形分析得:OP=2或![]() +1
+1
∴当t=2或![]() +1秒时,以M、P、O、C为顶点得四边形是平行四边形。
+1秒时,以M、P、O、C为顶点得四边形是平行四边形。


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案科目:初中数学 来源: 题型:
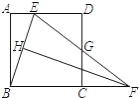
【题目】如图,在正方形ABCD中,点E是AD上的点,点F是BC的延长线上一点,CF=DE,连结BE和EF,EF与CD交于点G,且∠FBE=∠FEB.
(1)过点F作FH⊥BE于点H,证明:![]() ;
;
(2)猜想:BE、AE、EF之间的数量关系,并证明你的结论;
(3)若DG=2,求AE值.
查看答案和解析>>
科目:初中数学 来源: 题型:
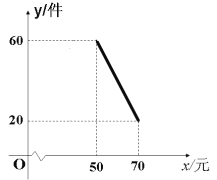
【题目】某商店试销一种新商品,该商品的进价为40元/件,经过一段时间的试销发现,每月的销售量会因售价在40~70元之间的调整而不同。当售价在40~50元时,每月销售量都为60件;当售价在50~70元时,每月销售量与售价的关系如图所示,令每月销售量为y件,售价为x元/件,每月的总利润为Q元。
(1)当售价在50~70元时,求每月销售量为y与x的函数关系式?
(2)当该商品售价x是多少元时,该商店每月获利最大,最大利润是多少元?
(3)若该商店每月采购这种新商品的进货款不低于1760元,则该商品每月最大利润为 元。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,真命题是( ) .
A. 对角线相等的四边形是矩形;
B. 对角线互相垂直的四边形是菱形;
C. 对角线互相平分的四边形是平行四边形;
D. 对角线互相垂直平分的四边形是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题是真命题的是( )
A. 过直线外一点可以画无数条直线与已知直线平行
B. 如果甲看乙的方向是北偏东60°,那么乙看甲的方向是南偏西30°
C. 3条直线交于一点,对顶角最多有6对
D. 与同一条直线相交的两条直线相交
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com