
【题目】已知∠MAN=90°,在射线AM上取一点B,在射线AN上取一点C,连接BC,再作点A关于直线BC的对称点D,连接AD、BD,移动点C,当2AD=BC时,∠ABD的度数是_____.

【答案】30 或150
【解析】
分两种情况,取BC的中点E,连接AE,DE,依据直角三角形斜边上中线的性质,即可得到△ADE是等边三角形,进而依据轴对称的性质得出∠ABD的度数.
解:分两种情况:
如图,当AB>AC时,取BC的中点E,连接AE,DE,
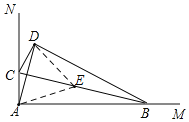
则AE=DE=![]() BC,
BC,
即BC=2AE=2DE,
又∵BC=2AD,
∴AD=AE=DE,
∴△ADE是等边三角形,
∴∠AED=60°,
又∵BC垂直平分AD,
∴∠AEC=30°,
又∵BE=AE,
∴∠ABC=![]() ∠AEC=15°,
∠AEC=15°,
∴∠ABD=2∠ABC=30°;
如图,当AB<AC时,同理可得∠ACD=30°,
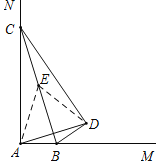
又∵∠BAC=∠BDC=90°,
∴∠ABD=150°,
故答案为:30°或150°.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图,四幅图象分别表示变量之间的关系,请按图象的顺序,将下面的四种情境与之对应排序.正确的顺序是( )

①篮球运动员投篮时,投出去的篮球的高度与时间的关系
②去超市购买同一单价的水果,所付费用与水果数量的关系
③李老师使用的是一种含月租的手机计费方式,则他每月所付话费与通话时间的关系
④周末,小明从家到图书馆,看了一段时间书后,按原速度原路返回,小明离家的距离与时间的关系
A. ①②③④ B. ①③④② C. ①③②④ D. ①④②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是一块锐角三角形材料,高线AH长8 cm,底边BC长10 cm,要把它加工成一个矩形零件,使矩形DEFG的一边EF在BC上,其余两个顶点D,G分别在AB,AC上,则四边形DEFG的最大面积为( )

A. 40 cm2 B. 20 cm2
C. 25 cm2 D. 10 cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
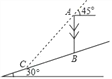
【题目】如图,在一个坡角为30°的斜坡上有一电线杆AB,当太阳光与水平线成45°角时,测得该杆在斜坡上的影长BC为20m.求电线杆AB的高(精确到0.1m,参考数值:![]() ≈1.73,
≈1.73,![]() ≈1.41).
≈1.41).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABD和△BCD都是等边三角形纸片,AB=2,将△ABD纸片翻折,使点A落在CD的中点E处,折痕为FG,点F、G分别在边AB、AD上.
(1)求证:△FBE是直角三角形;
(2)求BF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】证明命题“对角线相等的平行四边形是矩形”,要根据题意,画出图形,并用符号表示已知和求证,写出证明过程,下面是小张同学根据题意画出的图形,并写出了不完整的已知和求证.
已知:如图,ABCD是平行四边形,AC与BD是对角线,且 .
求证: .
请你补全已知和求证,并写出证明过程.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学之道在于悟,希望同学们在问题(1)解决过程中有所感悟,再继续探索研究问题(2)(3).
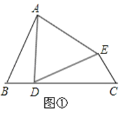
(1)如图①,D在线段BC上,∠B=∠C=∠ADE,AD=DE.求证:△ABD≌△DCE.
(2)如图②,△ABC是等腰直角三角形,∠ACB=90°,AC=BC=4,在CB的延长线上有一动点D,连接AD,以AD为直角边作等腰直角三角形ADE(∠ADE=90°,AD=DE ),连接EB并延长,与AC的延长线交于点F.当动点D在运动过程中,CF的长度是否会发生变化,如果变化,请说明理由;如果不变,请求出CF的长.
(3)如图③,射线AM与BN,MA⊥AB,NB⊥AB,点P是AB上一点, PA=1,PB=2,在射线AM与BN上分别作点C、点D,满足△CPD为等腰直角三角形.则△CPD的面积为 .


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点![]() 经过某种变换后得到点
经过某种变换后得到点![]() ,我们把点
,我们把点![]()
![]() 叫做点
叫做点![]() 的终结点.已知点
的终结点.已知点![]() 的终结点为
的终结点为![]() ,点
,点![]() 的终结点为
的终结点为![]() ,点
,点![]() 的终结点为
的终结点为![]() ,这样依次得到
,这样依次得到![]() 、
、![]() 、
、![]() 、
、![]() …
…![]() ,若点
,若点![]() 的坐标为
的坐标为![]() ,则点
,则点![]() 的坐标为( )
的坐标为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,□ABCD中,∠ABC为锐角,AB<BC,点E是AD上的一点,延长CE到F,连接BF交AD于点G, 使∠FBC=∠DCE.
⑴ 求证:∠D=∠F;
⑵ 在直线AD找一点P,使以点B、P、C为顶点的三角形与以点C、D、P为顶点的三角形相似.(在原图中标出准确P点的位置,必要时用直尺和圆规作出P点,保留作图的痕迹,不写作法)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com