
【题目】如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,延长AE交BC的延长线于点F.

(1)求证:△DAE≌△CFE;
(2)若AB=BC+AD,求证:BE⊥AF.
【答案】(1)见解析;(2)见解析
【解析】
(1)根据AD∥BC可知∠ADC=∠ECF,再根据E是CD的中点可求出△ADE≌△FCE;
(2)由(1)知△ADE≌△FCE,得到AE=EF,AD=CF,由于AB=BC+AD,等量代换得到AB=BC+CF,即AB=BF,证得△ABE≌△FBE,即可得到结论.
证明:(1)∵AD∥BC(已知),
∴∠ADC=∠ECF(两直线平行,内错角相等),
∵E是CD的中点(已知),
∴DE=EC(中点的定义).
∵在△ADE与△FCE中,
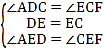 ,
,
∴△ADE≌△FCE(ASA);
(2)由(1)知△ADE≌△FCE,
∴AE=EF,AD=CF,
∵AB=BC+AD,
∴AB=BC+CF,
即AB=BF,
在△ABE与△FBE中,
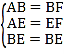 ,
,
∴△ABE≌△FBE(SSS),
∴∠AEB=∠FEB=90°,
∴BE⊥AF.


 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:初中数学 来源: 题型:
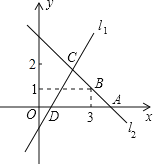
【题目】如图,直线l1:y=2x﹣2与x轴交于点D,直线l2:y=kx+b与x轴交于点A,且经过点B,直线l1,l2交于点C(m,2).
(1)求m的值;
(2)求直线l2的解析式;
(3)根据图象,直接写出1<kx+b<2x﹣2的解集.
(4)求△ACD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
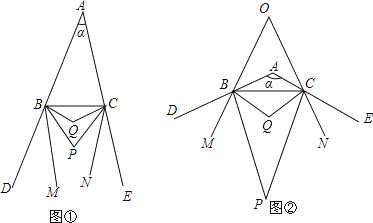
【题目】已知如图①,BP、CP分别是△ABC的外角∠CBD、∠BCE的角平分线,BQ、CQ分别是∠PBC、∠PCB的角平分线,BM、CN分别是∠PBD、∠PCE的角平分线,∠BAC=α.
(1)当α=40°时,∠BPC= °,∠BQC= °;
(2)当α= °时,BM∥CN;
(3)如图②,当α=120°时,BM、CN所在直线交于点O,求∠BOC的度数;
(4)在α>60°的条件下,直接写出∠BPC、∠BQC、∠BOC三角之间的数量关系: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了传承中华优秀传统文化,市教育局决定开展“经典诵读进校园”活动,某校团委组织八年级100名学生进行“经典诵读”选拔赛,赛后对全体参赛学生的成绩进行整理,得到下列不完整的统计图表。
组别 | 分数段 | 频次 | 频率 |
A | 60x<70 | 17 | 0.17 |
B | 70x<80 | 30 | a |
C | 80x<90 | b | 0.45 |
D | 90x<100 | 8 | 0.08 |
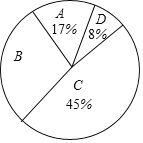
请根据所给信息,解答以下问题:
(1)表中a=___,b=___;
(2)请计算扇形统计图中B组对应扇形的圆心角的度数;
(3)已知有四名同学均取得98分的最好成绩,其中包括来自同一班级的甲、乙两名同学,学校将从这四名同学中随机选出两名参加市级比赛,请用列表法或画树状图法求甲、乙两名同学都被选中的概率。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某养殖户每年的养殖成本包括固定成本和可变成本,其中固定成本每年均为![]() 万元,可变成本逐年增长,已知该养殖户第
万元,可变成本逐年增长,已知该养殖户第![]() 年的可变成本为
年的可变成本为![]() 万元,第
万元,第![]() 年的养殖成本为
年的养殖成本为![]() 万元,现在要求可变成本平均每年增长的百分率,我们可设可变成本平均的每年增长的百分率为
万元,现在要求可变成本平均每年增长的百分率,我们可设可变成本平均的每年增长的百分率为![]() ,则可列方程为________.
,则可列方程为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边三角形 ABC 的边长为 3,过点 B 的直线 l⊥AB,且△ABC 与△A′BC′关于直线 l 对称,D 为线段 BC′上一动点,则 AD+CD 的最小值是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),在四边形ABCD中,已知∠ABC+∠ADC=180°,AB=AD,AB⊥AD,点E在CD的延长线上,且∠BAC=∠DAE.
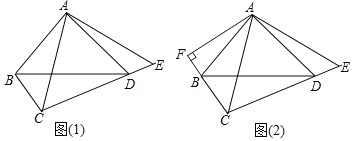
(1)求证:AC=AE;
(2)求证:CA平分∠BCD;
(3)如图(2),设AF是△ABC的边BC上的高,试求CE与AF之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知平行四边形ABCD,对角线AC,BD相交于点O,∠OBC=∠OCB.
(1)求证:平行四边形ABCD是矩形;
(2)请添加一个条件使矩形ABCD为正方形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,M(m,n)且m、n满足m2+2n2﹣2mn+4n+4=0,B(0,b)为y轴上一动点,绕B点将直线BM顺时针旋转45°交x轴于点C,过C作AC⊥BC交直线BM于点A(a,t).

(1)求点M的坐标;
(2)如图1,在B点运动的过程中,A点的横坐标是否会发生变化?若不变,求a的值;若变化,写出A点的横坐标a的取值范围;
(3)如图2,过T(a,0)作TH⊥BM(垂足H在x轴下方),在射线HB上截取HK=HT,连OK,求∠OKB的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com