
【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=30°,将△ABC绕点C按顺时针方向旋转n度后,得到△DEC,点D刚好落在AB边上. 
(1)求n的值;
(2)若F是DE的中点,判断四边形ACFD的形状,并说明理由.
【答案】
(1)解:∵在Rt△ABC中,∠ACB=90°,∠B=30°,将△ABC绕点C按顺时针方向旋转n度后,得到△DEC,
∴AC=DC,∠A=60°,
∴△ADC是等边三角形,
∴∠ACD=60°,
∴n的值是60
(2)解:四边形ACFD是菱形;
理由:∵∠DCE=∠ACB=90°,F是DE的中点,
∴FC=DF=FE,
∵∠CDF=∠A=60°,
∴△DFC是等边三角形,
∴DF=DC=FC,
∵△ADC是等边三角形,
∴AD=AC=DC,
∴AD=AC=FC=DF,
∴四边形ACFD是菱形
【解析】(1)利用旋转的性质得出AC=CD,进而得出△ADC是等边三角形,即可得出∠ACD的度数;(2)利用直角三角形的性质得出FC=DF,进而得出AD=AC=FC=DF,即可得出答案.


科目:初中数学 来源: 题型:
【题目】如图,CD是一高为4米的平台,AB是与CD底部相平的一棵树,在平台顶C点测得树顶A点的仰角α=30°,从平台底部向树的方向水平前进3米到达点E,在点E处测得树顶A点的仰角β=60°,求树高AB(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆货车和一辆小轿车同时从甲地出发,货车匀速行驶至乙地,小轿车中途停车休整后提速行驶至乙地,货车行驶的路程y1(km),小轿车行驶的路程y2(km)与时间x(h)的对应关系如图所示,下列结论错误的是( )

A. 甲、乙两地相距420km
B. y1=60x,y2=![]()
C. 货车出发4.5h与小轿车首次相遇
D. 两车首次相遇时距乙地150km
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电器商销售一种微波炉和电磁炉,微波炉每台定价![]() 元,电磁炉每台定价
元,电磁炉每台定价![]() 元.“双十一”期间商场决定开展促销活动,活动期间向客户提供两种优惠方案.
元.“双十一”期间商场决定开展促销活动,活动期间向客户提供两种优惠方案.
方案一:买一台微波炉送一台电磁炉;
方案二:微波炉和电磁炉都按定价的![]() 付款.
付款.
现某客户要到该卖场购买微波炉![]() 台,电磁炉
台,电磁炉![]() 台
台![]() .
.
![]() 若该客户按方案一购买,需付款________元.(用含
若该客户按方案一购买,需付款________元.(用含![]() 的代数式表示)若该客户按方案二购买,需付款________元.(用含
的代数式表示)若该客户按方案二购买,需付款________元.(用含![]() 的代数式表示)
的代数式表示)
![]() 若
若![]() 时,通过计算说明此时按哪种方案购买较为合算?
时,通过计算说明此时按哪种方案购买较为合算?
![]() 当
当![]() 时,你能给出一种更为省钱的购买方案吗?试写出你的购买方法.
时,你能给出一种更为省钱的购买方案吗?试写出你的购买方法.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是两块完全一样的含30°角的直角三角尺,分别记做△ABC与△A′B′C′,现将两块三角尺重叠在一起,设较长直角边的中点为M,绕中点M转动上面的三角尺ABC,使其直角顶点C恰好落在三角尺A′B′C′的斜边A′B′上.当∠A=30°,AC=10时,两直角顶点C,C′间的距离是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在ABCD中,AB=10,BC=14,E,F分别为边BC,AD上的点,若四边形AECF为正方形,则AE的长为( )
A.7
B.4或10
C.5或9
D.6或8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在合肥大蜀山山顶有一斜坡AP的坡度为1∶2.4,坡长AP为26米,在坡顶A处的同一水平面上有一座安徽卫视发射塔BC,在斜坡底P处测得该塔的塔顶B的仰角为45°,在坡顶A处测得该塔的塔顶B的仰角为76°,求:
(1)坡顶A到地面PQ的距离;
(2)发射塔BC的高度(结果保留为整数,参考数据:sin76°≈0.97,cos76°≈0.24,tan76°≈4.01,tan14°≈0.25).

![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,AB=4,tan∠ACB=![]() ,点D、E分别是BC、AD的中点,AF∥BC交CE的延长线于点F,则四边形AFBD的面积为______.
,点D、E分别是BC、AD的中点,AF∥BC交CE的延长线于点F,则四边形AFBD的面积为______.
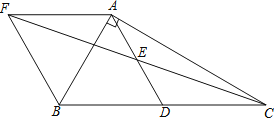
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com