
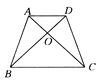
【题目】如图所示,在四边形ABCD中,已知AB与 CD不平行,∠ABD=∠ACD,请你添加一个条件:______ ,使的加上这个条件后能够推出AD∥BC ,且AB=CD.
【答案】∠DAC=∠ADB或∠BAD=∠CDA或∠DBC=∠ACB或∠ABC=∠DCB或OB=OC或OA=OD.
【解析】试题分析:先证四边形AECO是梯形,再说明是等腰梯形.由题意可知,∠ABD=∠ACD,AD是△BAD和△CDA的公共边,则可以再添加一组角∠DAC=∠ADB或∠BAD=∠CDA,同理可添加∠DBC=∠ACB,∠ABC=∠DCB,OB=OC,OA=OD,从而推出AD∥BC且AB=CD.
由题意可知,∠ABD=∠ACD,AD是△BAD和△CDA的公共边,
则可以再添加一组角∠DAC=∠ADB或∠BAD=∠CDA
∴△BAD≌△CDA
∴BD=AC,AB=DC,
∵∠DAC=∠ADB,
∴OA=OD,
∴OB=OC,
∴∠OBC=∠OCB,
∵∠AOD=∠BOC,
∴∠DAC=∠ACB=∠ADB=∠DBC,
∴AD∥BC
同理可添加∠DBC=∠ACB,∠ABC=∠DCB,OB=OC,OA=OD,从而推出AD∥BC且AB=CD.
本题答案不唯一,如∠DAC=∠ADB,∠BAD=∠CDA,∠DBC=∠ACB,∠ABC=∠DCB,OB=OC,OA=OD.(任选其一)


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】
(1)计算:3( ![]() ﹣π)0﹣
﹣π)0﹣ ![]() +(﹣1)2011
+(﹣1)2011
(2)先化简,再求值: ![]() ,其中x=
,其中x= ![]() -3.
-3.
(3)如图,平行四边形ABCD的对角线AC、BD交于点O,E、F在AC上,G、H在BD上,且AF=CE,BH=DG. 求证:GF∥HE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,点A为x轴负半轴上一点,点B为x轴正半轴上一点,C(0,a),D(b,a),其中a,b满足关系式:|a+3|+(b-a+1)2=0.
(1)a=___,b=___,△BCD的面积为______;
(2)如图2,若AC⊥BC,点P线段OC上一点,连接BP,延长BP交AC于点Q,当∠CPQ=∠CQP时,求证:BP平分∠ABC;
(3)如图3,若AC⊥BC,点E是点A与点B之间一动点,连接CE,CB始终平分∠ECF,当点E在点A与点B之间运动时,![]() 的值是否变化?若不变,求出其值;若变化,请说明理由.
的值是否变化?若不变,求出其值;若变化,请说明理由.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小英和小明姐弟二人准备一起去观看端午节龙舟赛.但因家中临时有事,必须留下一人在家,于是姐弟二人采用游戏的方式来确定谁去看龙舟赛.游戏规则是:在不透明的口袋中分别放入2个白色和1个黄色的乒乓球,它们除颜色外其余都相同.游戏时先由小英从口袋中任意摸出1个乒乓球记下颜色后放回并摇匀,再由小明从口袋中摸出1个乒乓球,记下颜色.如果姐弟二人摸到的乒乓球颜色相同.则小英赢,否则小明赢.
(1)请用树状图或列表的方法表示游戏中所有可能出现的结果.
(2)这个游戏对游戏双方公平吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x、y的方程组![]() (实数m是常数).
(实数m是常数).
(1)若x+y=1,求实数m的值;
(2)若-1≤x-y≤5,求m的取值范围;
(3)在(2)的条件下,化简:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】同学们,我们曾经研究过n×n的正方形网格,得到了网格中正方形的总数的表达式为12+22+32+…+n2 . 但n为100时,应如何计算正方形的具体个数呢?下面我们就一起来探究并解决这个问题.首先,通过探究我们已经知道0×1+1×2+2×3+…+(n﹣l)×n
= ![]() n(n+1)(n﹣1)时,我们可以这样做:
n(n+1)(n﹣1)时,我们可以这样做:
(1)观察并猜想:
12+22=(1+0)×1+(1+1)×2=l+0×1+2+1×2=(1+2)+(0×1+1×2)
12+22+32=(1+0)×1+(1+1)×2+(l+2)×3
=1+0×1+2+1×2+3+2×3
=(1+2+3)+(0×1+1×2+2×3)
12+22+32+42=(1+0)×1+(1+1)×2+(l+2)×3+
=1+0×1+2+1×2+3+2×3+
=(1+2+3+4)+()
…
(2)归纳结论:
12+22+32+…+n2=(1+0)×1+(1+1)×2+(1+2)×3+…[1+(n﹣l)]n
=1+0×1+2+1×2+3+2×3+…+n+(n﹣1)×n
=()+[]
=+
= ![]() ×
×
(3)实践应用:
通过以上探究过程,我们就可以算出当n为100时,正方形网格中正方形的总个数是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电脑经销商计划同时购进一批电脑机箱和液晶显示器,若购进电脑机箱10台,和液晶显示器8台,共需要资金7000元,若购进电脑机箱两台和液晶显示器5台,共需要资金4120元.
(1)每台电脑机箱、液晶显示器的进价各是多少元?
(2)该经销商计划购进这两种商品共50台,而可用于购买这两种商品的资金不超过22240元,根据市场行情,销售电脑机箱,液晶显示器一台分别可获得10元和160元,改经销商希望销售完这两种商品,所获得利润不少于4100元,试问:该经销商有几种进货方案?哪种方案获利最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC是等腰直角三角形,∠A=90°,D是腰AC上的一个动点,过C作CE垂直于BD或BD的延长线,垂足为E,如图. 
(1)若BD是AC的中线,求 ![]() 的值;
的值;
(2)若BD是∠ABC的角平分线,求 ![]() 的值;
的值;
(3)结合(1)、(2),试推断 ![]() 的取值范围(直接写出结论,不必证明),并探究
的取值范围(直接写出结论,不必证明),并探究 ![]() 的值能小于
的值能小于 ![]() 吗?若能,求出满足条件的D点的位置;若不能,说明理由.
吗?若能,求出满足条件的D点的位置;若不能,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com