
【题目】如图,已知A(-4,![]() )、B(2,-4)是一次函数
)、B(2,-4)是一次函数![]() 的图象和反比例函数
的图象和反比例函数![]() 的图象的两个交点.
的图象的两个交点.
(1)求反比例函数和一次函数的解析式;
(2)求直线AB和![]() 轴的交点C的坐标;
轴的交点C的坐标;
(3)求方程![]() 的解(请直接写出答案);
的解(请直接写出答案);
(4)求不等式![]() 的解集(请直接写出答案).
的解集(请直接写出答案).

【答案】(1)![]() ,
,![]() ;(2)C点坐标为(-2,0);(3)
;(2)C点坐标为(-2,0);(3)![]() 或2;(4)
或2;(4)![]() 或
或![]()
【解析】
(1)根据待定系数法就可以求出函数的解析式;
(2)求直线![]() 与
与![]() 轴的交点坐标,令
轴的交点坐标,令![]() 时,求解自变量
时,求解自变量![]() 的值即可,
的值即可,
(3)求方程![]() 的解即是求函数y=kx+b以函数
的解即是求函数y=kx+b以函数![]() 的交点的横坐标.
的交点的横坐标.
(4)利用图像直接![]() 的解集.
的解集.
(1)∵B(2,-4)在函数![]() 的图象上,
的图象上,
∴m=-8.
∴反比例函数的解析式为:![]() .
.
∵点A(-4,n)在函数![]() 的图象上,
的图象上,
∴n=2, ∴A(-4,2),
∵y=kx+b经过A(-4,2),B(2,-4),
∴![]() ,解之得:
,解之得:![]()
∴一次函数的解析式为:![]()
(2)当-x-2=0时,x=-2,
∴C点坐标为(-2,0)
(3)![]() ,
,
![]()
相当于一次函数y=kx+b的图象和反比例函数![]() 的图象的交点的横坐标,
的图象的交点的横坐标,
结合函数图形可知:
![]() 或
或![]()
(4)![]() ,
,
![]()
即一次函数值小于反比例函数值,根据图像可得:
-4<x<0或x>2.


科目:初中数学 来源: 题型:
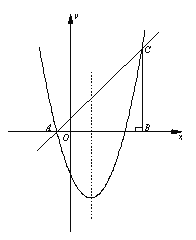
【题目】如图,在平面直角坐标系中,△ABC的边AB在x轴上,∠ABC=90°,AB=BC,OA=1,OB=4,抛物线![]() 经过A、C两点.
经过A、C两点.
(1)求抛物线的解析式及其顶点坐标;
(2)如图①,点P是抛物线上位于x轴下方的一点,点Q与点P关于抛物线的对称轴对称,过点P、Q分别向x轴作垂线,垂足为点D、E,记矩形DPQE的周长为d,求d的最大值,并求出使d最大值时点P的坐标;
(3)如图②,点M是抛物线上位于直线AC下方的一点,过点M作MF⊥AC于点F,连接MC,作MN∥BC交直线AC于点N,若MN将△MFC的面积分成2:3两部分,请确定M点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
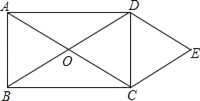
【题目】如图所示,O为矩形ABCD对角线的交点,DE∥AC,CE∥BD.
(1)试判断四边形OCED的形状,并说明理由;
(2)若AB=3,BC=4,求四边形OCED的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AF∥CD,CB平分∠ACD,BD平分∠EBF,且BC⊥BD,下列结论:① BC平分∠ABE;② AC∥BE;③ ∠CBE+∠D=90°;④ ∠DEB=2∠ABC.其中正确结论的个数有( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与反比例函数y=![]() 的图象交于点A(﹣3,m+8),B(n,﹣6)两点.
的图象交于点A(﹣3,m+8),B(n,﹣6)两点.
(1)求一次函数与反比例函数的解析式;
(2)求△AOB的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(x1,y1)、B(x2,y2)在二次函数y=x2+mx+n的图象上,当x1=1、x2=3时,y1=y2.
(1)①求m;②若抛物线与x轴只有一个公共点,求n的值.
(2)若P(a,b1),Q(3,b2)是函数图象上的两点,且b1>b2,求实数a的取值范围.
(3)若对于任意实数x1、x2都有y1+y2≥2,求n的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
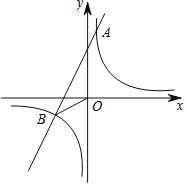
【题目】如图,已知反比例函数![]() 与一次函数
与一次函数![]() 的图象交于点A(1,8)、B(-4,m).
的图象交于点A(1,8)、B(-4,m).
(1)求k1、k2、b的值;
(2)求△AOB的面积;
(3)请直接写出不等式![]() 的解集;
的解集;
(4)若M(x1,y1)、N(x2,y2)是反比例函数![]() 图象上的两点,且x1<x2,y1<y2,指出点M、N各位于哪个象限,并说明理由.
图象上的两点,且x1<x2,y1<y2,指出点M、N各位于哪个象限,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
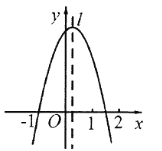
【题目】如图,抛物线y=ax2+bx+c经过点(![]() 1,0),对称轴为l.则下列结论:①abc>0; ②a-b+c=0; ③2a+c<0; ④a+b<0,其中所有正确的结论是______________
1,0),对称轴为l.则下列结论:①abc>0; ②a-b+c=0; ③2a+c<0; ④a+b<0,其中所有正确的结论是______________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读并解决问题:有趣的勾股数组
定义:一般地,若三角形三边长![]() ,
,![]() ,
,![]() 都是正整数,且满足
都是正整数,且满足![]() ,那么数组
,那么数组![]() 称为勾股数组.
称为勾股数组.
关于勾股数组的研究我国历史上有过非常辉煌的成就,根据我国古代数学书《周髀算经》记载,在约公元前1100年,人们就已经知道“勾广三,股修四,径隅五”(古人把较短的直角边称为勾,较长直角边称为股,而斜边则成称为弦),即知道了勾股数组![]() ,后来人们发现并证明了勾股定理.
,后来人们发现并证明了勾股定理.
公元263年魏朝刘徽注《九章算术》,文中除提到勾股数组![]() 以外,还提到
以外,还提到![]() ,
,![]() ,
,![]() ,
,![]() 等勾股数组.
等勾股数组.
设![]() ,
,![]() 是两个正整数,且
是两个正整数,且![]() ,三角形三边长
,三角形三边长![]() ,
,![]() ,
,![]() 都是正整数.
都是正整数.
下表中的![]() ,
,![]() ,
,![]() 可以组成一些有规律的勾股数组
可以组成一些有规律的勾股数组![]() :
:
|
|
|
|
|
2 | 1 | 3 | 4 | 5 |
3 | 2 | 5 | 12 | 13 |
4 | 1 | 15 | 8 | 17 |
4 | 3 | 7 | 24 | 25 |
5 | 2 | 21 | 20 | 29 |
5 | 4 | 9 | 40 | 41 |
6 | 1 | 35 | 12 | 37 |
6 | 5 | 11 | 60 | 61 |
7 | 2 | 45 | 28 | 53 |
7 | 4 | 33 | 56 | 65 |
7 | 6 | 13 | 84 | 85 |
请你仔细观察这个表格,解答下列问题:
(1)表中![]() 和
和![]() ,
,![]() 的等量关系式是________;
的等量关系式是________;
(2)表中的勾股数组用只含![]() ,
,![]() 的代数式表示为________;
的代数式表示为________;
(3)小明通过研究表中数据发现:若勾股数组中,弦与股的差为1,则勾股数的形式可表述为![]() (
(![]() ,
,![]() 为正整数),请你用含
为正整数),请你用含![]() 的代数式表示
的代数式表示![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com