
【题目】在![]() ABCD中,E、F分别是AD、BC上的点,将平行四边形ABCD沿EF所在直线翻折,使点B与点D重合,且点A落在点A′处.
ABCD中,E、F分别是AD、BC上的点,将平行四边形ABCD沿EF所在直线翻折,使点B与点D重合,且点A落在点A′处.
(1)求证:△A′ED≌△CFD;
(2)连结BE,若∠EBF=60°,EF=3,求四边形BFDE的面积.

【答案】(1)见解析;(2)![]() .
.
【解析】
由由翻折可知:AB=A′D,∠ABC=∠A′DF,∠EFB=∠EFD,由平行四边形的性质知,AB=CD,∠ABC=∠ADC,进一步可证∠FDC=∠A′DE, A′D=CD.再结合平行线的性质说明ED=DF,即可证明△A′ED≌△CFD;
(2)先证明四边形EBFD为菱形,从而BE=BF=3.过点E作EH⊥BC于点H,根据锐角三角函数的知识求出EH的长,然后利用三角形面积公式计算即可.
(1)证明:由翻折可知:
AB=A′D,∠ABC=∠A′DF,∠EFB=∠EFD,
∵四边形ABCD是平行四边形,
∴AB=CD,∠ABC=∠ADC,
∴∠ADC=∠A′DF,
∴∠FDC=∠A′DE,
∵AB=A′D,AB=CD,
∴A′D=CD.
∵AD∥BC,
∴∠DEF=∠EFB,
∵∠EFB=∠EFD,
∴∠DEF=∠EFD,
∴ED=DF,
∴△A′ED≌△CFD;
(2)解:∵AD∥BC,A′B∥DF,
∴四边形EBFD为平行四边形.
由(1)DE=DF,
∴四边形EBFD为菱形.
∵∠EBF=60°,
∴△BEF为菱形.
∵EF=3,
∴BE=BF=3.
过点E作EH⊥BC于点H,
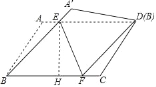
∴四边形BFDE的面积为:sin60°AEBF=![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,∠ABC和∠ACB的角平分线相交于点P,且PE⊥AB,PF⊥AC,垂足分别为E、F
(1)求证:PE=PF;
(2)若∠BAC=60°,连接AP,求∠EAP的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察图,先填空,然后回答问题

(1)由上而下第![]() 行的白球与黑球总数比第
行的白球与黑球总数比第![]() 行多 个.若第
行多 个.若第![]() 行白球与黑球的总数记作
行白球与黑球的总数记作![]() ,写出
,写出![]() 与
与![]() 的关系式.
的关系式.
(2)求出第![]() 行白球与黑球的总数可能是
行白球与黑球的总数可能是![]() 个吗?如果是,求出
个吗?如果是,求出![]() 的值;如果不是,说明理由.
的值;如果不是,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=(t+1)x2+2(t+2)x+![]() 在x=0和x=2时的函数值相等
在x=0和x=2时的函数值相等
(1)求二次函数的解析式,并作图象;
(2)若一次函数y=kx+6的图象与二次函数的象都经过点A(﹣3,m),求m和k的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”.已知点A、B、C、D分别是“果圆”与坐标轴的交点,抛物线的解析式为y=(x﹣1)2﹣4,AB为半圆的直径,则这个“果圆”被y轴截得的弦CD的长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的七边形ABCDEFG中,∠1、∠2、∠3、∠4 四个角的外角和为180°,∠5 的外角为60°,BP、DP 分别平分∠ABC、∠CDE,则∠BPD 的度数是( )

A. 130° B. 120° C. 110° D. 100°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与
与![]() 轴、
轴、![]() 轴分别相交于点C、B,与直线
轴分别相交于点C、B,与直线![]() 相交于点A.
相交于点A.
(1)求A点坐标;
(2)如果在y轴上存在一点P,使△OAP是以OA为底边的等腰三角形,求P点坐标;
(3)在直线![]() 上是否存在点Q,使△OAQ的面积等于6?若存在,请求出Q点的坐标,若不存在,请说明理由.
上是否存在点Q,使△OAQ的面积等于6?若存在,请求出Q点的坐标,若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等腰![]() 和等腰
和等腰![]() 中,
中,![]() ,
,![]() ,连接
,连接![]() 交于点
交于点![]() .
.
(1)如图1,若![]() :
:
①![]() 与
与![]() 的数量关系为 ;
的数量关系为 ;
②![]() 的度数为 ;
的度数为 ;
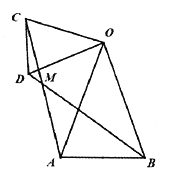
图1
(2)如图2,若![]() :
:
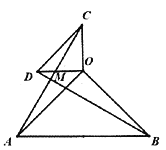
图2
①判断![]() 与
与![]() 之间存在怎样的数量关系?并说明理由;
之间存在怎样的数量关系?并说明理由;
②求![]() 的度数;
的度数;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A为某旅游景区的最佳观景点,游客可以在B处乘坐缆车沿BD方向先到达小观景平台DE观景,然后再由E处继续乘坐缆车沿EA方向到达A处,返程时从A处乘坐升降电梯直接到C处.已知AC⊥BC于C,DE∥BC,斜坡BD的坡度i=4:3,BC=210米,DE=48米,BD=100米,α=64°,则AC的高度为( )米(结果精确到0.1米,参考数据:sin64°≈0.9,tan64°≈2.1)

A. 214.2 B. 235.2 C. 294.2 D. 315.2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com