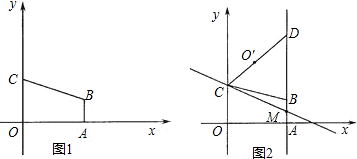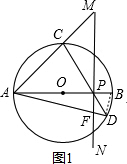
(1)证明:连接BD
∵AB是⊙O直径,
∴∠ADB=90°.
∴∠ADC+∠BDC=90°.
∵MN⊥AB,
∴∠AEP+∠BAC=90°.
∵∠BAC=∠BDC,
∴∠ADC=∠AEP.
∵∠DPF=∠EPC,
∴△PDF∽△PEC.
∴
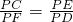
即PC•PD=PE•PF.
(2)解:结论仍然成立.
证明:连接BD.

∵AB是⊙O直径,
∴∠ADB=90°.
∴∠ABD+∠BAD=90°.
∵∠ACD=∠PCE,∠ABD=∠ACD,
∴∠PCE+∠BAD=90°.
∵MN⊥AB,
∴∠PFA+∠BAD=90°.
∴∠PCE=∠PFA.
∵∠EPC=∠FPD,
∴△PCE∽△PFD.
∴
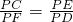
,
∴PC•PD=PE•PF.
(3)解:结论仍然成立.
证明:连接AC.
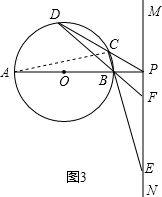
∵AB是⊙O直径,
∴∠ACB=90°,
∴∠A+∠ABC=90°.
∵∠ABC=∠EBP,
∴∠A+∠EBP=90°.
∵MN⊥AB,
∴∠PEB+∠EBP=90°.
∴∠A=∠PEB.
∵∠A=∠D,
∴∠D=∠PEB.
∵∠DPF=∠EPC,
∴△DPF∽△EPC.
∴
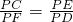
.
∴PC•PD=PE•PF.
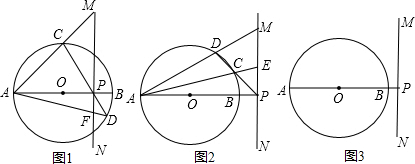
分析:(1)本题要证的实际是△ECP与△DFP相似.已知对顶角∠CPE=∠DPF,要想证相似就要再找出一组相等的对应角;
连接BD.根据圆周角定理可得∠BAC=∠CDB,因此根据等角的余角相等,即可得出∠PDF=∠DEP;由此可证出△PDF∽△PEC,根据相似三角形对应线段成比例,即可得出PC•PD=PE•PF.
(2)还成立,证法与(1)大致相同,只不过证三角形相似时,已知的不是对顶角,而是一个公共角.
(3)依然成立,还是通过证△ECP与△DFP相似,来求解.这两个三角形中已知了一个公共角,按(1)的思路,可连接AC,那么∠D=∠A,而∠A和∠PEB是一组对顶角的余角,因此∠A=∠PEB=∠D,由此可证得两三角形相似,即可证得(1)的结论.
点评:本题主要考查了圆周角定理,相似三角形的判定和性质等知识点;根据圆周角定理得出的角相等,来证得三角形相似是解题的关键.

 (1)证明:连接BD
(1)证明:连接BD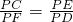

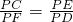 ,
,
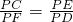 .
.