
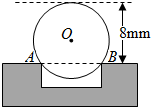
 工程上常用钢珠来测量零件上小圆孔的宽口,假设钢珠的直径是10mm,测得钢珠顶端离零件表面的距离为8mm,如图所示.
工程上常用钢珠来测量零件上小圆孔的宽口,假设钢珠的直径是10mm,测得钢珠顶端离零件表面的距离为8mm,如图所示.分析 (1)如图,在⊙O上取一点C,连接AC,作线段AC、AB的垂直平分线,它们的交点即为圆心O
(2)在Rt△OAG中,利用勾股定理即可解决问题.
解答 解:(1)如图,在⊙O上取一点C,连接AC,作线段AC、AB的垂直平分线,它们的交点即为圆心O.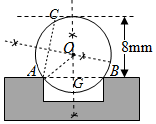
(2)作OG⊥AB于G,则AG=GB,
∵OA=5,OG=8=5=3,
在Rt△AOG中,AG=$\sqrt{A{O}^{2}-O{G}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4,
∴AB=2AG=8.
点评 本题的考查作图-应用与设计、圆、垂径定理、勾股定理等知识,解题的关键是掌握找圆心的方法,学会添加常用辅助线,构造直角三角形解决实际问题,属于中考常考题型.


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
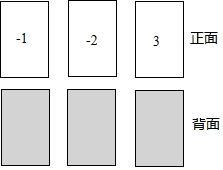 有3张不透明的卡片,除正面写有不同的数字外,其它均相同.将这三张卡片背面朝上洗匀后,第一次从中随机抽取一张,并把这张卡片标有的数字记作一次函数表达式中的k,第二次从余下的两张卡片中再随机抽取一张,上面标有的数字记作一次函数表达式中的b
有3张不透明的卡片,除正面写有不同的数字外,其它均相同.将这三张卡片背面朝上洗匀后,第一次从中随机抽取一张,并把这张卡片标有的数字记作一次函数表达式中的k,第二次从余下的两张卡片中再随机抽取一张,上面标有的数字记作一次函数表达式中的b查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
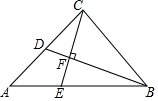 如图,△ABC中,CA=CB,∠ACB=90°,BD平分∠ABC交AC于D,CE⊥BD于F,交AB于E.
如图,△ABC中,CA=CB,∠ACB=90°,BD平分∠ABC交AC于D,CE⊥BD于F,交AB于E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com