
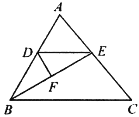
【题目】如图,在△ABC 中,BE 平分∠ABC,DE∥BC.
(1)判断△DBE 是什么三角形,并说明理由;
(2)若 F 为 BE 中点,∠ABC=58°,试说明 DF⊥BE,并求∠EDF 的度数.
【答案】(1)△DBE是等腰三角形,理由见详解;(2)证明见详解,∠EDF=61°.
【解析】
(1)由BE 平分∠ABC可得∠DBE=∠CBE,又DE∥BC,即可判断∠DBE=∠CBE,即可得到结论;
(2)由(1)知,△DBE是等腰三角形,点F是BE中点,即可判断DF⊥BE;由∠ABC=58°,可以得到∠ABE=∠BED=29°,利用余角性质,即可得到∠EDF的度数.
解:(1)△DBE是等腰三角形.
理由是:
∵BE平分∠ABC,
∴∠DBE=∠CBE,
∵DE∥BC,
∴∠DEB=∠CBE=∠DBE,
∴BD=DE,
∴△DBE是等腰三角形;
(2)由(1)知,△DBE是等腰三角形,
又点F是BE中点,
由等腰三角形三线合一定理,得:DF⊥BE;
∴∠DFE=90°,
∵∠ABC=58°,
∴∠ABE =29°=∠BED
∴∠EDF=90°-29°=61°.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】学校与图书馆在同一条笔直道路上,甲从学校去图书馆,乙从图书馆回学校,甲、乙两人都匀速步行且同时出发,乙先到达目的地.两人之间的距离y(米)与时间t(分钟)之间的函数关系如图所示.

(1)根据图象信息,当t= 分钟时甲乙两人相遇,甲的速度为 米/分钟,乙的速度为 米/分钟;
(2)图中点A的坐标为 ;
(3)求线段AB所直线的函数表达式;
(4)在整个过程中,何时两人相距400米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD是边长为4的正方形,点E在边AD所在的直线上,连接CE,以CE为边,作正方形CEFG(点D,点F在直线CE的同侧),连接BF,
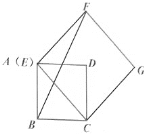
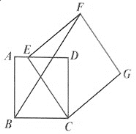
图1 图2
(1)如图1,当点E与点A重合时,则![]() _____;
_____;
(2)如图2,当点E在线段AD上时,![]() ,
,
①求点F到AD的距离;
②求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形纸片ABCD沿对角线BD折叠,使点A落在平面上的F点处,DF交BC于点E.
(1)求证:△DCE≌△BFE;
(2)若CD=2,∠ADB=30°,求BE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
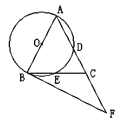
【题目】如图,在△ABC中,AB=AC,∠BAC=54°,以AB为直径的 ⊙O分别交AC,BC于点D,E,过点B作⊙O的切线,交AC的延长线于点F.
(1)求证:BE=CE;
(2)求∠CBF的度数;
(3)若AB=6,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
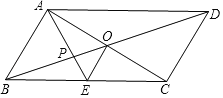
【题目】如图,平行四边形ABCD的对角线AC、BD相交于点O,AE平分∠BAD,分别交BC、BD于点E、P,连接OE,∠ADC=60°,AB=![]() BC=1,则下列结论:
BC=1,则下列结论:
①∠CAD=30°②BD=![]() ③S平行四边形ABCD=ABAC④OE=
③S平行四边形ABCD=ABAC④OE=![]() AD⑤S△APO=
AD⑤S△APO=![]() ,正确的个数是( )
,正确的个数是( )
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级有800名学生,在一次跳绳模拟测试中,从中随机抽取部分学生,根据其测试成绩制作了下面两个统计图,请根据相关信息,解答下列问题:

(1)本次抽取到的学生人数为______,扇形统计图中![]() 的值为______.
的值为______.
(2)本次调查获取的样本数据的众数是_____(分),中位数是_____(分).
(3)根据样本数据,估计我校八年级模拟体测中得12分的学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图像与反比例函数y=![]() 的图像交于点,A(n,3)和点B(1,-6),与y轴交于点C.
的图像交于点,A(n,3)和点B(1,-6),与y轴交于点C.
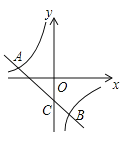
(1)求一次函数和反比例函数表达式;
(2)请直接写出关于x的不等式kx+b>![]() 的解集;
的解集;
(3)把点C绕着点O逆时针旋转90°,得到点![]() ,连接
,连接![]() ,
,![]() ,求△AB
,求△AB![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
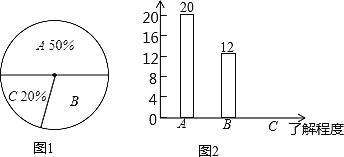
【题目】双峰县教育局要求各学校加强对学生的安全教育,全县各中小学校引起高度重视,小刚就本班同学对安全知识的了解程度进行了一次调查统计.他将统计结果分为三类,A:熟悉;B:了解较多;C:一般了解。图①和图②是他采集数据后,绘制的两幅不完整的统计图,请你根据图中提供的信息解答以下问题:
(1)求小刚所在的班级共有多少名学生;
(2)在条形图中,将表示“一般了解”的部分补充完整‘’
(3)在扇形统计图中,计算“了解较多”部分所对应的扇形圆心角的度数;
(4)如果小刚所在年级共1000名同学,请你估算全年级对安全知识“了解较多”的学生人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com