
分析 由平行四边形的性质易证两三角形相似,但是由于点F的位置未定,需分类讨论.分两种情况:(1)点F在线段AB上时;(2)点F在线段BA的延长线上时.
解答 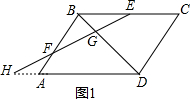 解:(1)如图1,点F在线段AB上时,设EF与DA的延长线交于H,
解:(1)如图1,点F在线段AB上时,设EF与DA的延长线交于H,
∵BC∥AD,
∴△EBF∽△HAF,
∴HA:BE=AF:BF=1:2,
即HA=$\frac{1}{2}$BE
∵BC∥AD,
∴△DHG∽△BEG,
∴BG:DG=BE:DH
∵BC=AD=2BE,
∴DH=AD+AH=2BE+$\frac{1}{2}$BE=$\frac{5}{2}$BE,
∴$\frac{GD}{GB}$=$\frac{5}{2}$;
(2)如图2,点F在线段BA的延长线上时,设EF与DA交于H,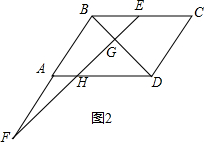 ∵BC∥AD,
∵BC∥AD,
∴△EBF∽△HAF,
∴HA:BE=AF:BF=1:2,
即HA=$\frac{1}{2}$BE,
∵BC∥AD,
∴△DHG∽△BEG,
∴BG:DG=BE:DH
∵BC=AD=2BE,
∴DH=AD+AH=2BE-$\frac{1}{2}$BE=$\frac{3}{2}$BE,
∴$\frac{GD}{GB}$=$\frac{3}{2}$.
故答案为:$\frac{5}{2}$或$\frac{3}{2}$.
点评 本题考查了相似三角形的性质以及分类讨论的数学思想;其中由相似三角形的性质得出比例式是解题关键.注意:求相似比不仅要认准对应边,还需注意两个三角形的先后次序.


科目:初中数学 来源: 题型:选择题
| A. | $2\sqrt{2}-1$ | B. | $2-\sqrt{2}$ | C. | $1-\sqrt{2}$ | D. | $2+\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,点E为正方形ABCD中AD边上的动点,AB=2,以BE为边画正方形BEFG,连结CF和CE,则△CEF面积的最小值为$\frac{3}{2}$.
如图,点E为正方形ABCD中AD边上的动点,AB=2,以BE为边画正方形BEFG,连结CF和CE,则△CEF面积的最小值为$\frac{3}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
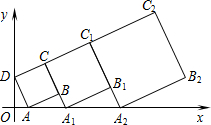 在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1,作第1个正方形A1B1C1C;延长C1B1交x轴于点A2,作第2个正方形A2B2C2C1,…,按这样的规律进行下去,第2016个正方形的面积是5×($\frac{3}{2}$)4030.
在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1,作第1个正方形A1B1C1C;延长C1B1交x轴于点A2,作第2个正方形A2B2C2C1,…,按这样的规律进行下去,第2016个正方形的面积是5×($\frac{3}{2}$)4030.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com